题目内容
19.化简求值:$\frac{1}{x-2}•\frac{{x}^{2}-4}{x}-\frac{1+x}{{x}^{2}+x}$,其中x=$\sqrt{2}-1$.分析 先根据分式混合运算的法则把原式进行化简,再把x的值代入进行计算即可.
解答 解:原式=$\frac{1}{x-2}$•$\frac{(x+2)(x-2)}{x}$-$\frac{x+1}{x(x+1)}$
=$\frac{x+2}{x}$-$\frac{1}{x}$
=$\frac{x+1}{x}$,
当x=$\sqrt{2}$-1时,原式=$\frac{\sqrt{2}-1+1}{\sqrt{2}-1}$=$\sqrt{2}$+2.
点评 本题考查的是分式的化简求值,熟知分式混合运算的法则是解答此题的关键.

练习册系列答案
 阳光课堂同步练习系列答案
阳光课堂同步练习系列答案
相关题目
7.如果两圆的半径长分别为1和3,圆心距为3,那么这两个圆的位置关系是( )
| A. | 内含 | B. | 内切 | C. | 外切 | D. | 相交 |
11. 将四个棱长为1的正方体如图摆放,则这个几何体的表面积是( )
将四个棱长为1的正方体如图摆放,则这个几何体的表面积是( )
 将四个棱长为1的正方体如图摆放,则这个几何体的表面积是( )
将四个棱长为1的正方体如图摆放,则这个几何体的表面积是( )| A. | 3 | B. | 9 | C. | 12 | D. | 18 |
8.下列计算正确的是( )
| A. | $\root{3}{27}$=3 | B. | -(-3)2=9 | C. | -(-2)0=1 | D. | |-3|=-3 |
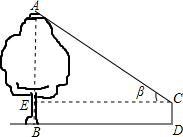 小亮和小红在公园放风筝,不小心让风筝挂在树梢上,风筝固定在A处(如图),为测量此时风筝的高度,他俩按如下步骤操作:
小亮和小红在公园放风筝,不小心让风筝挂在树梢上,风筝固定在A处(如图),为测量此时风筝的高度,他俩按如下步骤操作: 在某公益活动中,小明对本年级同学的捐款情况进行了统计,绘制成如图所示的不完整的统计图,其中捐10元的人数占年级总人数的25%,则本次捐款20元的人数为35人.
在某公益活动中,小明对本年级同学的捐款情况进行了统计,绘制成如图所示的不完整的统计图,其中捐10元的人数占年级总人数的25%,则本次捐款20元的人数为35人.