题目内容
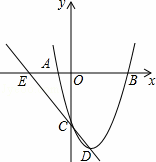
如图,已知抛物线经过点A(﹣2,0)、B(4,0)、C(0,﹣8).
(1)求抛物线的解析式及其顶点D的坐标;
(2)直线CD交x轴于点E,过抛物线上在对称轴的右边的点P,作y轴的平行线交x轴于点F,交直线CD于M,使PM= EF,请求出点P的坐标;
EF,请求出点P的坐标;
(3)将抛物线沿对称轴平移,要使抛物线与(2)中的线段EM总有交点,那么抛物线向上最多平移多少个单位长度,向下最多平移多少个单位长度.
解:(1)根据题意可设抛物线的解析式为y=a(x+2)(x﹣4).
∵点C(0,﹣8)在抛物线y=a(x+2)(x﹣4)上,
∴﹣8a=﹣8.
∴a=1.
∴y=(x+2)(x﹣4)
=x2﹣2x﹣8
=(x﹣1)2﹣9.
∴抛物线的解析式为y=x2﹣2x﹣8,顶点D的坐标为(1,﹣9).
(2)如图,
设直线CD的解析式为y=kx+b.
∴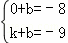
解得: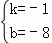 .
.
∴直线CD的解析式为y=﹣x﹣8.
当y=0时,﹣x﹣8=0,
则有x=﹣8.
∴点E的坐标为(﹣8,0).
设点P的坐标为(m,n),
则PM=(m2﹣2m﹣8)﹣(﹣m﹣8)=m2﹣m,EF=m﹣(﹣8)=m+8.
∵PM=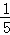 EF,
EF,
∴m2﹣m=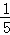 (m+8).
(m+8).
整理得:5m2﹣6m﹣8=0.
∴(5m+4)(m﹣2)=0
解得:m1=﹣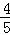 ,m2=2.
,m2=2.
∵点P在对称轴x=1的右边,
∴m=2.
此时,n=22﹣2×2﹣8=﹣8.
∴点P的坐标为(2,﹣8).
(3)当m=2时,y=﹣2﹣8=﹣10.
∴点M的坐标为(2,﹣10).
设平移后的抛物线的解析式为y=x2﹣2x﹣8+c,
①若抛物线y=x2﹣2x﹣8+c与直线y=﹣x﹣8相切,
则方程x2﹣2x﹣8+c=﹣x﹣8即x2﹣x+c=0有两个相等的实数根.
∴(﹣1)2﹣4×1×c=0.
∴c=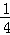 .
.
②若抛物线y=x2﹣2x﹣8+c经过点M,
则有22﹣2×2﹣8+c=﹣10.
∴c=﹣2.
③若抛物线y=x2﹣2x﹣8+c经过点E,
则有(﹣8)2﹣2×(﹣8)﹣8+c=0.
∴c=﹣72.
综上所述:要使抛物线与(2)中的线段EM总有交点,抛物线向上最多平移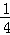 个单位长度,向下最多平移72个单位长度.
个单位长度,向下最多平移72个单位长度.


已知方程 ﹣a=
﹣a= ,且关于x的不等式组
,且关于x的不等式组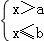 只有4个整数解,那么b的取值范围是( )
只有4个整数解,那么b的取值范围是( )
|
| A. | ﹣1<b≤3 | B. | 2<b≤3 | C. | 8≤b<9 | D. | 3≤b<4 |
下列几何体中,有一个几何体的主视图与俯视图的形状不一样,这个几何体是( )
|
| A. |
正方体 | B. |
圆柱 | C. |
圆锥 | D. |
球 |
 前
前 项和为
项和为 ,且
,且 求
求 .
. ,求
,求
 )﹣1﹣|
)﹣1﹣| ﹣8|+2cos60°.
﹣8|+2cos60°.




 ,则t的值是()
,则t的值是()
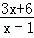 <0
<0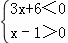 或②
或②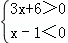
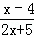 ≤0
≤0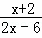 >0.
>0.