题目内容
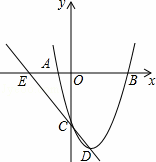
已知:直线y=ax+b与抛物线y=ax2﹣bx+c的一个交点为A(0,2),同时这条直线与x轴相交于点B,且相交所成的角β为45°.
(1)求点B的坐标;
(2)求抛物线y=ax2﹣bx+c的解析式;
(3)判断抛物线y=ax2﹣bx+c与x轴是否有交点,并说明理由.若有交点设为M,N(点M在点N左边),将此抛物线关于y轴作轴反射得到M的对应点为E,轴反射后的像与原像相交于点F,连接NF,EF得△DEF,在原像上是否存在点P,使得△NEP的面积与△NEF的面积相等?若存在,请求出点P的坐标;若不存在,请说明理由.
解:(1)∵直线y=ax+b过A(0,2),同时这条直线与x轴相交于点B,且相交所成的角β为45°,
∴OA=OB,
∴当a>0时,B(﹣2,0),当a<0时,B(2,0);
(2)把A(0,2),B(﹣2,0)代入直线y=ax+b得;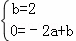 ,
,
解得: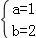 ,
,
把A(0,2),B(2,0)代入直线y=ax+b得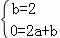 ,
,
解得: ,
,
∵抛物线y=ax2﹣bx+c过A(0,2),
∴c=2,
∴抛物线的解析式为:y=x2+2x+2或y=﹣x2+2x+2.
(3)存在.
如图,抛物线为y=x2+2x+2时,b2﹣4ac=4﹣4×1×2<0,抛物线与x轴没有交点,
抛物线为y=﹣x2+2x+2时,b2﹣4ac=4﹣4×(﹣1)×2>0,抛物线与x轴有两个交点;
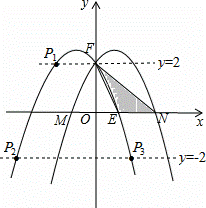
∵轴反射后的像与原像相交于点F,则F点即为A点,
∴F(0,2)
∵△NEP的面积与△NEF的面积相等且同底,
∴P点的纵坐标为2或﹣2,
当y=2时,﹣x2﹣2x+2=2,解得:x=﹣2或x=0(与点F重合,舍去);
当y=﹣2时,﹣x2﹣2x+2=﹣2,解得:x=﹣1+ ,x=﹣1﹣
,x=﹣1﹣ ,
,
∴存在满足条件的点P,点P坐标为:(﹣2,2),(﹣1+ ,﹣2),(﹣1﹣
,﹣2),(﹣1﹣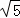 ,﹣2).
,﹣2).

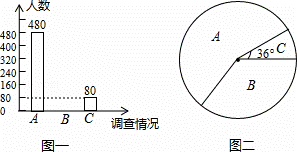
学校“清洁校园”环境爱护志愿者的年龄分布如图,那么这些志愿者年龄的众数是( )

|
| A. | 12岁 | B. | 13岁 | C. | 14岁 | D. | 15岁 |
不等式组 的解集是( )
的解集是( )
|
| A. | x≥﹣1 | B. | x≤2 | C. | 1≤x≤2 | D. | ﹣1≤x≤2 |

 B.
B.
 D.
D.
 EF,请求出点P的坐标;
EF,请求出点P的坐标;