题目内容
20.如图,在平面直角坐标系中,点C的坐标为(0,4),动点A以每秒1个单位长的速度,从点O出发沿x轴的正方向运动,M是线段AC的中点.将线段AM以点A为中心,沿顺时针方向旋转90°,得到线段AB,过点B作x轴的垂线,垂足为E,过点C作y轴的垂线,交直线BE于点D,运动时间为t秒.(1)当点B与点D重合时,求t的值;
(2)当t为何值时,S△BCD=$\frac{25}{4}$?
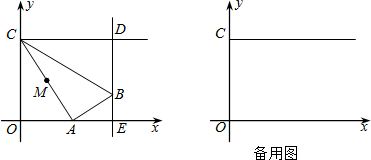
分析 (1)由于∠CAB=90°,易证得Rt△CAO∽Rt△ABE;当B、D重合时,BE的长已知(即OC长),根据AC、AB的比例关系,即可得到AO、BE的比例关系,由此求得t的值.
(2)求△BCD的面积时,可以CD为底、BD为高来解,那么表示出BD的长是关键;Rt△CAO∽Rt△ABE,且知道AC、AB的比例关系,即可通过相似三角形的对应边成比例求出BE的长,进一步得到BD的长,在表达BD长时,应分两种情况考虑:①B在线段DE上,②B在ED的延长线上.
解答 解:(1)∵∠CAO+∠BAE=90°,∠ABE+∠BAE=90°,
∴∠CAO=∠ABE.
∴Rt△CAO∽Rt△ABE.
∴$\frac{CA}{CB}=\frac{AO}{BE}$.
∴$\frac{2AB}{AB}=\frac{t}{4}$.
∴t=8.
(2)由Rt△CAO∽Rt△ABE可知:BE=$\frac{1}{2}$t,AE=2.
当0<t<8时,S△BCD=$\frac{1}{2}$CD•BD=$\frac{1}{2}$(2+t)(4-$\frac{t}{2}$)=$\frac{25}{4}$.
∴t1=t2=3.
当t>8时,S△BCD=$\frac{1}{2}$CD•BD=$\frac{1}{2}$(2+t)($\frac{t}{2}$-4)=$\frac{25}{4}$.
∴${t}_{1}=3+5\sqrt{2}$,${t}_{2}=3-5\sqrt{2}$(为负数,舍去).
当t=3或3+5$\sqrt{2}$时,${S}_{△BCD}=\frac{25}{4}$.
点评 考查了二次函数综合题,该题是图形的动点问题,解决本题的关键在于找出相似三角形,得到关键线段的表达式,注意点在运动过程中未知数的取值范围问题.

 愉快的寒假南京出版社系列答案
愉快的寒假南京出版社系列答案| A. | $\frac{1}{3}$ | B. | -$\frac{1}{3}$ | C. | 3 | D. | -3 |
| A. | $\frac{1}{x}$<x<x2 | B. | x<x2<$\frac{1}{x}$ | C. | x2<x<$\frac{1}{x}$ | D. | $\frac{1}{x}$<x2<x |
| A. | x>-2 | B. | x<-2 | C. | x≥-2 | D. | x≤-2 |
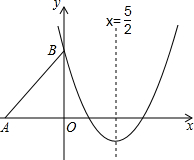 如图,Rt△ABO的两直角边OA、OB分别在x轴的负半轴和y轴的正半轴上,O为坐标原点,A、B两点的坐标分别为(-3,0)、(0,4),抛物线y=$\frac{2}{3}$x2+bx+c经过点B,且顶点在直线x=$\frac{5}{2}$上.
如图,Rt△ABO的两直角边OA、OB分别在x轴的负半轴和y轴的正半轴上,O为坐标原点,A、B两点的坐标分别为(-3,0)、(0,4),抛物线y=$\frac{2}{3}$x2+bx+c经过点B,且顶点在直线x=$\frac{5}{2}$上.
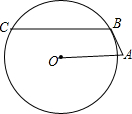 如图,AB切⊙O于点B,OA=2$\sqrt{3}$,∠BAO=60°,弦BC∥OA,则$\widehat{BC}$的长为2π(结果保留π).
如图,AB切⊙O于点B,OA=2$\sqrt{3}$,∠BAO=60°,弦BC∥OA,则$\widehat{BC}$的长为2π(结果保留π).