题目内容
6.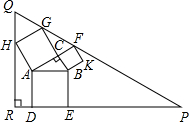 如图,Rt△ABC中,∠ACB=90°,∠BAC=30°,AB=4,分别以AB、BC、AC为边作正方形ABED、BCFK、ACGH,再作Rt△PQR,使∠R=90°,点H在边QR上,点D、E在边PR上,点G、F在边PQ上,则PQ的长为14+4$\sqrt{3}$.
如图,Rt△ABC中,∠ACB=90°,∠BAC=30°,AB=4,分别以AB、BC、AC为边作正方形ABED、BCFK、ACGH,再作Rt△PQR,使∠R=90°,点H在边QR上,点D、E在边PR上,点G、F在边PQ上,则PQ的长为14+4$\sqrt{3}$.
分析 首先证明△ABC≌△GFC(SAS),利用全等三角形的性质可得:∠CGF=∠BAC=30°,在直角△ABC中,根据三角函数即可求得AC,进而由等边三角形的性质和正方形的性质及三角函数就可求得QR的长,在直角△QRP中运用三角函数即可得到RP、进而可求出PQ的长.
解答  解:延长BA交QR于点M,连接AR,AP.
解:延长BA交QR于点M,连接AR,AP.
在△ABC和△GFC中
$\left\{\begin{array}{l}{AC=GC}\\{∠ACB=∠GCF}\\{BC=FC}\end{array}\right.$,
∴△ABC≌△GFC(SAS),
∴∠CGF=∠BAC=30°,
∴∠HGQ=60°,
∵∠HAC=∠BAD=90°,
∴∠BAC+∠DAH=180°,
又∵AD∥QR,
∴∠RHA+∠DAH=180°,
∴∠RHA=∠BAC=30°,
∴∠QHG=60°,
∴∠Q=∠QHG=∠QGH=60°,
∴△QHG是等边三角形.
AC=AB•cos30°=4×$\frac{\sqrt{3}}{2}$=2$\sqrt{3}$,
则QH=HA=HG=AC=2$\sqrt{3}$,
在直角△HMA中,HM=AH•sin60°=2$\sqrt{3}$×$\frac{\sqrt{3}}{2}$=3,AM=HA•cos60°=$\sqrt{3}$,
在直角△AMR中,MR=AD=AB=4.
∴QR=2$\sqrt{3}$+3+4=7+2$\sqrt{3}$,
∴QP=2QR=14+4$\sqrt{3}$.
故答案为:14+4$\sqrt{3}$.
点评 本题考查了勾股定理和含30度角的直角三角形以及全等三角形的判定和性质,题目的综合性较强,难度较大,正确运用三角函数以及勾股定理是解决本题的关键.

练习册系列答案
 特高级教师点拨系列答案
特高级教师点拨系列答案
相关题目
18.盐城市中学开展“唱红歌”比赛活动,九年级(1)、(2)班根据初赛成绩,各选出5名选手参加复赛,两个班各选出的5名选手的复赛成绩(满分为100分)如图所示.
(1)根据图示填写下表;
(2)结合两班复赛成绩的平均数和中位数,分析哪个班级的复赛成绩较好;
(3)计算两班复赛成绩的方差.(方差公式:s2=$\frac{1}{n}$[(x1-$\overline{x}$)2+(x2-$\overline{x}$)2+…+(xn-$\overline{x}$)2].
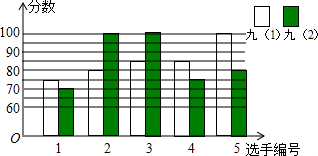
(1)根据图示填写下表;
| 班级 | 平均数(分) | 中位数(分) | 众数(分) |
| 九(1) | 85 | 85 | 85 |
| 九(2) | 85 | 80 | 100 |
(3)计算两班复赛成绩的方差.(方差公式:s2=$\frac{1}{n}$[(x1-$\overline{x}$)2+(x2-$\overline{x}$)2+…+(xn-$\overline{x}$)2].

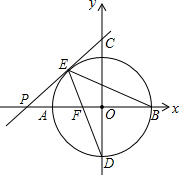 ⊙O交坐标轴于A、B、C、D四点,P为x轴上一点,PE切⊙O于E,连接ED、EB,PA=4,PE=8
⊙O交坐标轴于A、B、C、D四点,P为x轴上一点,PE切⊙O于E,连接ED、EB,PA=4,PE=8

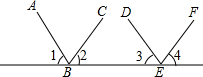 完成下列推理说明:
完成下列推理说明: