题目内容
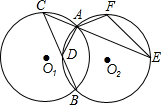 如图,半径为1的等圆⊙O1与⊙O2相交于A、B两点,点C从点A出发,在⊙O1,上逆时针运动;同时点F从点A出发,在⊙O2上顺时针运动,两点的运动速度相同,⊙O1的弦CB交⊙O2于点D.
如图,半径为1的等圆⊙O1与⊙O2相交于A、B两点,点C从点A出发,在⊙O1,上逆时针运动;同时点F从点A出发,在⊙O2上顺时针运动,两点的运动速度相同,⊙O1的弦CB交⊙O2于点D.(1)求证:AD=AF;
(2)若O1O2=
| 2 |
分析:(1)连接AB,BF,得出
=
,再根据⊙O1与⊙O2是等圆,得出∠ABC=∠ABF,即可证出AD=AF;
(2)连接O1B,O2B,O1C,O2E,O1O2,BE,根据⊙O1与⊙O2的弧AB相等,得出∠C=∠E,BC=BE,再证出△O1BC≌△O2BE,得出∠O1BC=∠O2BE,∠CBE=∠O1BO2,再根据O1O2=
,
O1B=O2B=1,得出O1O2B为等腰直角三角形,∠CBE=∠O1BO2=90°,从而证出△CBE也为等腰直角三角形,即可得出CE=
BC.
 |
| AC |
 |
| AF |
(2)连接O1B,O2B,O1C,O2E,O1O2,BE,根据⊙O1与⊙O2的弧AB相等,得出∠C=∠E,BC=BE,再证出△O1BC≌△O2BE,得出∠O1BC=∠O2BE,∠CBE=∠O1BO2,再根据O1O2=
| 2 |
O1B=O2B=1,得出O1O2B为等腰直角三角形,∠CBE=∠O1BO2=90°,从而证出△CBE也为等腰直角三角形,即可得出CE=
| 2 |
解答:解:(1)连接AB,BF,
∵C从点A出发,点F从点A出发,两点的运动速度相同,
∴
=
,
∵⊙O1与⊙O2是等圆,
∴∠ABC=∠ABF,
∴AD=AF;
(2)连接O1B,O2B,O1C,O2E,O1O2,BE,
∵⊙O1与⊙O2的弧AB相等,
∴∠C=∠E,
∴BC=BE,
在△O1BC和△O2BE中,
∴△O1BC≌△O2BE(SSS),
∴∠O1BC=∠O2BE,∠CBE=∠O1BO2,
∵O1O2=
,
O1B=O2B=1,
∴O1O2B为等腰直角三角形,
∴∠CBE=∠O1BO2=90°,
∴△CBE也为等腰直角三角形,
∴CE=
BC.
∵C从点A出发,点F从点A出发,两点的运动速度相同,

∴
 |
| AC |
 |
| AF |
∵⊙O1与⊙O2是等圆,
∴∠ABC=∠ABF,
∴AD=AF;
(2)连接O1B,O2B,O1C,O2E,O1O2,BE,
∵⊙O1与⊙O2的弧AB相等,
∴∠C=∠E,
∴BC=BE,
在△O1BC和△O2BE中,
|
∴△O1BC≌△O2BE(SSS),
∴∠O1BC=∠O2BE,∠CBE=∠O1BO2,
∵O1O2=
| 2 |
O1B=O2B=1,
∴O1O2B为等腰直角三角形,
∴∠CBE=∠O1BO2=90°,
∴△CBE也为等腰直角三角形,
∴CE=
| 2 |
点评:此题考查了圆的综合,用到的知识点是全等三角形的判定与性质、圆的有关性质、等腰三角形的判定与性质,关键是作出辅助线,证出△CBE也为等腰直角三角形.

练习册系列答案
相关题目
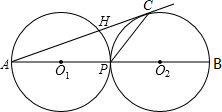 如图,外切于P点的⊙O1和⊙O2是半径为3cm的等圆,连心线交⊙O1于点A,交⊙O2于点B,AC与⊙O2相切于点C,连接PC,则PC的长为( )
如图,外切于P点的⊙O1和⊙O2是半径为3cm的等圆,连心线交⊙O1于点A,交⊙O2于点B,AC与⊙O2相切于点C,连接PC,则PC的长为( )A、2
| ||
B、3
| ||
| C、3cm | ||
| D、4.5cm |
 如图,三个半径为r的等圆两两外切,且与△ABC的三边分别相切,求△ABC的边长.(结果保留π)
如图,三个半径为r的等圆两两外切,且与△ABC的三边分别相切,求△ABC的边长.(结果保留π) 15、如图:有六个半径为1的等圆按图所示摆放(相邻两圆均外切),六圆的连心线构成等边三角形,则圆心线外侧的6个扇形(阴影部分)的面积是
15、如图:有六个半径为1的等圆按图所示摆放(相邻两圆均外切),六圆的连心线构成等边三角形,则圆心线外侧的6个扇形(阴影部分)的面积是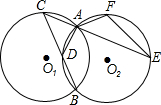 如图,半径为1的等圆⊙O1与⊙O2相交于A、B两点,点C从点A出发,在⊙O1,上逆时针运动;同时点F从点A出发,在⊙O2上顺时针运动,两点的运动速度相同,⊙O1的弦CB交⊙O2于点D.
如图,半径为1的等圆⊙O1与⊙O2相交于A、B两点,点C从点A出发,在⊙O1,上逆时针运动;同时点F从点A出发,在⊙O2上顺时针运动,两点的运动速度相同,⊙O1的弦CB交⊙O2于点D. ,射线CA交⊙O2于点E,试探究CE与CB之间的数量关系.
,射线CA交⊙O2于点E,试探究CE与CB之间的数量关系.