��Ŀ����
��֪���κ���L1��y1=x2+6x+5k��L2��y2=kx2+6kx+5k������k��0��1��
��1��д���йض��κ���L1��L2�������е����ʽ��ۣ�
��2��������������L1��L2�ཻ�ڵ�E��F����k��ֵ�����仯ʱ�����ж��߶�EF�ij����Ƿ����仯����˵�����ɣ�
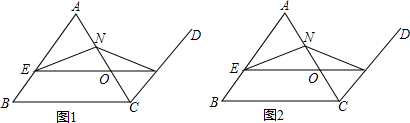
��3���ڣ�2���У������κ���L1 �Ķ���ΪM�����κ���L2�Ķ���ΪN��
�ٵ�kΪ��ֵʱ�ǣ���M��N����ֱ��EF�Գƣ�
���Ƿ����ʵ��k��ʹ��MN=2EF��������ڣ����ʵ��k����������ڣ���˵�����ɣ�
��1��д���йض��κ���L1��L2�������е����ʽ��ۣ�
��2��������������L1��L2�ཻ�ڵ�E��F����k��ֵ�����仯ʱ�����ж��߶�EF�ij����Ƿ����仯����˵�����ɣ�
��3���ڣ�2���У������κ���L1 �Ķ���ΪM�����κ���L2�Ķ���ΪN��
�ٵ�kΪ��ֵʱ�ǣ���M��N����ֱ��EF�Գƣ�
���Ƿ����ʵ��k��ʹ��MN=2EF��������ڣ����ʵ��k����������ڣ���˵�����ɣ�
���㣺���κ����ۺ���
ר�⣺�ۺ���
��������1��ֻ��Ӷ��κ����ĶԳ��ᡢ��y��Ľ���ȽǶȿ��ǾͿɽ�����⣻
��2������y1=y2�������E��F�ĺ����꣬�Ӷ��õ���E��F�����꣬���еõ�EF�ij����Ϳɽ�����⣻
��3���õ�M��N�����꼰ֱ��EF�Ĺ�ϵʽ��Ȼ�����������������k�ķ��̣��Ϳɽ�����⣮
��2������y1=y2�������E��F�ĺ����꣬�Ӷ��õ���E��F�����꣬���еõ�EF�ij����Ϳɽ�����⣻
��3���õ�M��N�����꼰ֱ��EF�Ĺ�ϵʽ��Ȼ�����������������k�ķ��̣��Ϳɽ�����⣮
����⣺��1�����κ���L1��L2�������е������ǣ�
�����ǵĶԳ�����ͬ������x=-3��
�����ǵ�ͼ����y��Ľ��㶼�ǣ�0��5k����
��2���߶�EF�ij��Ȳ������仯��
���ɣ���y1=y2ʱ��x2+6x+5k=kx2+6kx+5k��
�������k-1����x2+6x��=0��
��k��1����x2+6x=0��
��ã�x1=0��x2=-6��
�������E�ڵ�F����ߣ�
���E��������-6��5k������F��������0��5k����
��EF=|0-��-6��|=6��
���߶�EF�ij��Ȳ������仯��
��3������y1=x2+6x+5k=��x+3��2+5k-9��M��-3��5k-9����
��y2=kx2+6kx+5k=k��x+3��2-4k��N��-3��-4k����
��ֱ��EF�Ĺ�ϵʽΪy=5k���ҵ�M��N����ֱ��EF�Գƣ�
��-4k-5k=5k-��5k-9����
��ã�k=-1��
�൱kΪ-1ʱ����M��N����ֱ��EF�Գƣ�
�ڡ�MN=|��5k-9��-��-4k��|=|9k-9|��MN=2EF=12��
��|9k-9|=12��
���k1=
��k2=-
��
��ʵ��kΪ
��-
��
�����ǵĶԳ�����ͬ������x=-3��
�����ǵ�ͼ����y��Ľ��㶼�ǣ�0��5k����
��2���߶�EF�ij��Ȳ������仯��
���ɣ���y1=y2ʱ��x2+6x+5k=kx2+6kx+5k��
�������k-1����x2+6x��=0��
��k��1����x2+6x=0��
��ã�x1=0��x2=-6��
�������E�ڵ�F����ߣ�
���E��������-6��5k������F��������0��5k����
��EF=|0-��-6��|=6��
���߶�EF�ij��Ȳ������仯��
��3������y1=x2+6x+5k=��x+3��2+5k-9��M��-3��5k-9����
��y2=kx2+6kx+5k=k��x+3��2-4k��N��-3��-4k����
��ֱ��EF�Ĺ�ϵʽΪy=5k���ҵ�M��N����ֱ��EF�Գƣ�
��-4k-5k=5k-��5k-9����
��ã�k=-1��
�൱kΪ-1ʱ����M��N����ֱ��EF�Գƣ�
�ڡ�MN=|��5k-9��-��-4k��|=|9k-9|��MN=2EF=12��
��|9k-9|=12��
���k1=
| 7 |
| 3 |
| 1 |
| 3 |
��ʵ��kΪ
| 7 |
| 3 |
| 1 |
| 3 |
������������Ҫ�����˶��κ��������ʡ���һԪ���η��̡���ԳƵ����ʡ������ֵ���̵�֪ʶ����Ҫע����ǵ������������ͬʱ������֮��ľ���ӦΪ�������������ľ���ֵ��

��ϰ��ϵ�д�
 ��ѧȫ��������ѵ��ϵ�д�
��ѧȫ��������ѵ��ϵ�д�
�����Ŀ
 �������С��������ǵľ�ס�����ѳ�Ϊ���н����һ����Ҫ���ݣ�ij������������ͨ����Ǩ�ɷ���ֲ�ݡ������������ȴ�ʩ��ʹ�����̵�����������ӣ�����ͼ�����ṩ����Ϣ������˵��������ǣ�������
�������С��������ǵľ�ס�����ѳ�Ϊ���н����һ����Ҫ���ݣ�ij������������ͨ����Ǩ�ɷ���ֲ�ݡ������������ȴ�ʩ��ʹ�����̵�����������ӣ�����ͼ�����ṩ����Ϣ������˵��������ǣ�������| A��2009��������̵����Ϊ420���� |
| B��2011����̵����������� |
| C����2009�굽2012�꣬ÿ���̵�����������ʶ������� |
| D����2009�굽2012�꣬ÿ����̵������������ |
 ��ͼ��һ������������ʾ��ͼ�������ƬXY��35mm��������50mm��������5m��ľ����ж�������������70mm�أ�
��ͼ��һ������������ʾ��ͼ�������ƬXY��35mm��������50mm��������5m��ľ����ж�������������70mm�أ� ��ͼ����ABC�У�AD�����ߣ�AE�ǽ�ƽ���ߣ�CF��AE��F��AB=10��AC=6����DF�ij�Ϊ
��ͼ����ABC�У�AD�����ߣ�AE�ǽ�ƽ���ߣ�CF��AE��F��AB=10��AC=6����DF�ij�Ϊ ��ͼ��ʾ����ֱ�DZ߳�Ϊ6
��ͼ��ʾ����ֱ�DZ߳�Ϊ6