题目内容
如图，线段AD把△ABC分为面积相等的两部分，则线段AD是
- A.三角形的角平分线
- B.三角形的中线
- C.三角形的高
- D.以上都不对
B
分析：作三角形ABC的高AE，根据三角形面积公式，分别表示出S△ABD和S△ACD，即可得出BD=CD，即线段AD是三角形的中线．
解答：
解：作AE⊥BC，
∴S△ABD=
×BD×AE，
S△ACD=×CD×AE，
∵S△ABD=S△ACD，
即×BD×AE=×CD×AE，
∴BD=CD，
即线段AD是三角形的中线．
故选B．
点评：本题主要考查了三角形的面积和三角形的中线，三角形的中线可分三角形为面积相等的两部分．
分析：作三角形ABC的高AE，根据三角形面积公式，分别表示出S△ABD和S△ACD，即可得出BD=CD，即线段AD是三角形的中线．
解答：
解：作AE⊥BC，∴S△ABD=
×BD×AE，S△ACD=
×CD×AE，∵S△ABD=S△ACD，
即
×BD×AE=×CD×AE，∴BD=CD，
即线段AD是三角形的中线．
故选B．
点评：本题主要考查了三角形的面积和三角形的中线，三角形的中线可分三角形为面积相等的两部分．
练习册系列答案
天天向上一本好卷系列答案
小学生10分钟应用题系列答案
相关题目
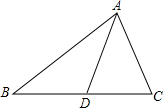如图，线段AD把△ABC分为面积相等的两部分，则线段AD是（ ）| A、三角形的角平分线 | B、三角形的中线 | C、三角形的高 | D、以上都不对 |
