题目内容
4.若(x-$\frac{1}{x}$)2=$\frac{9}{4}$,则x2-$\frac{1}{{x}^{2}}$=±$\frac{15}{4}$.分析 两边开方求出x-$\frac{1}{x}$,展开求出x2+$\frac{1}{{x}^{2}}$,根据完全平方公式求出(x+$\frac{1}{x}$)2,求出x+$\frac{1}{{x}^{2}}$,最后根据平方差公式分解,代入即可求出答案.
解答 解:∵(x-$\frac{1}{x}$)2=$\frac{9}{4}$,
∴x-$\frac{1}{x}$=±$\frac{3}{2}$,x2-2•x•$\frac{1}{x}$+$\frac{1}{{x}^{2}}$=$\frac{9}{4}$,
∴x2+$\frac{1}{{x}^{2}}$=$\frac{17}{4}$,
∴(x+$\frac{1}{x}$)2=x2+$\frac{1}{{x}^{2}}$+2=$\frac{25}{4}$,
∴x+$\frac{1}{x}$=$±\frac{5}{2}$,
当x-$\frac{1}{x}$=$\frac{3}{2}$,x+$\frac{1}{x}$=$\frac{5}{2}$时,x2-$\frac{1}{{x}^{2}}$=(x+$\frac{1}{x}$)(x-$\frac{1}{x}$)=$\frac{15}{4}$;
当x-$\frac{1}{x}$=$\frac{3}{2}$,x+$\frac{1}{x}$=-$\frac{5}{2}$时,x2-$\frac{1}{{x}^{2}}$=(x+$\frac{1}{x}$)(x-$\frac{1}{x}$)=-$\frac{15}{4}$;
当x-$\frac{1}{x}$=-$\frac{3}{2}$,x+$\frac{1}{x}$=$\frac{5}{2}$时,x2-$\frac{1}{{x}^{2}}$=(x+$\frac{1}{x}$)(x-$\frac{1}{x}$)=-$\frac{15}{4}$;
当x-$\frac{1}{x}$=-$\frac{3}{2}$,x+$\frac{1}{x}$=-$\frac{5}{2}$时,x2-$\frac{1}{{x}^{2}}$=(x+$\frac{1}{x}$)(x-$\frac{1}{x}$)=$\frac{15}{4}$;
故答案为:±$\frac{15}{4}$.
点评 本题考查了完全平方公式和平方差公式,能熟练地运用公式进行变形是解此题的关键.

 名校课堂系列答案
名校课堂系列答案| A. | -ab | B. | -3ab | C. | a | D. | -3a |
| A. | $\frac{5}{2}<r<4$ | B. | $\frac{5}{2}<r<3$ | C. | 3<r<4 | D. | r>3 |
| A. | 3.85x=67.6 | B. | 18×2.9+3.85(x-18)=67.6 | ||
| C. | 18×2.9+3.85x=67.6 | D. | 18×2.9+3.85(25-x)=67.6 |
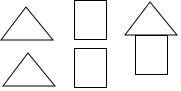 在拼图游戏中,从图的四张纸片中,任取两张纸片,能拼成“小房子”(如图)概率等于( )
在拼图游戏中,从图的四张纸片中,任取两张纸片,能拼成“小房子”(如图)概率等于( )| A. | 1 | B. | $\frac{2}{3}$ | C. | $\frac{1}{2}$ | D. | $\frac{1}{3}$ |
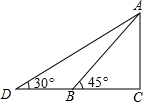 如图,幼儿园为了加强安全管理,决定将园内的滑滑梯的倾角由45°降为30°,已知原滑滑梯AB的长为5m,点D,B,C在同一水平地面上.
如图,幼儿园为了加强安全管理,决定将园内的滑滑梯的倾角由45°降为30°,已知原滑滑梯AB的长为5m,点D,B,C在同一水平地面上.