题目内容
12．
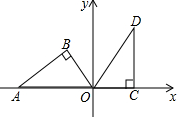如图，直角坐标系中，Rt△DOC的直角边OC在x轴上，∠OCD=90°，OD=6，OC=3，现将△DOC绕原点O按逆时针方向旋转，得到△AOB，且点A在x轴上．（1）请直接写出：∠A=30°°；
（2）请求出线段OD扫过的面积．
分析 （1）在Rt△DOC，根据特殊锐角三角函数值可知∠D=30°，由旋转的性质可知：∠A=∠D=30°；
（2）先求得旋转角∠AOD=120°，然后利用扇形的面积公式进行计算即可．
解答 解：在Rt△DOC，∠OCD=90°，OD=6，OC=3，
∴sin∠D=$\frac{OC}{OD}=\frac{1}{2}$．
∴∠D=30°，
由旋转的性质可知：∠A=∠D=30°．
（2）在Rt△DOC，∠OCD=90°，∠D=30°，
∴∠DOC=60°，
∴∠AOD=180°-60°=120°，
∴线段OD扫过的面积为$\frac{{120×π×{6^2}}}{360}=12π$．
点评 本题主要考查的是旋转的性质、特殊锐角三角函数值、扇形的面积公式，利用旋转的性质求得∠AOD的度数是解题的关键．
练习册系列答案
相关题目
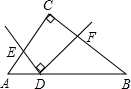如图，Rt△ABC中，∠ACB=90°，AC=3，BC=4，另一直角顶点D在如图位置关系在AB上运动，且两边分别交两直角边AC、BC于E，F两点．若D点到这两点线段长度之比为1：2，则AD=$\frac{15}{11}$．
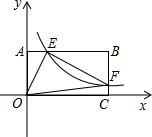如图，将一矩形OABC放在直角坐标系中，O为坐标原点，点A在y轴正半轴上，点E是边AB上的一个动点（不与点A、B重合），过点E的反比例函数y=$\frac{k}{x}$（x＞0）的图象与边BC交与点F．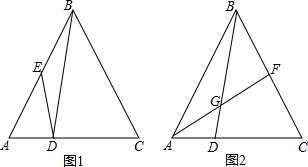
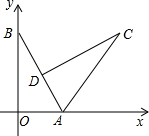如图，平面直角坐标系中，已知O为坐标原点，A（3，0），B（0，4）．将Rt△AOB绕点A顺时针旋转得到Rt△ACD，旋转后点D恰好落在AB边上时，则D点的坐标为（$\frac{6}{5}$，$\frac{12}{5}$）．
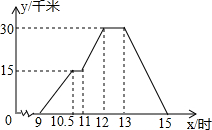李老师周末骑自行车去郊游，如图是他离家的距离y（千米）与时间t（时）之间关系的函数图象，李老师9时离开家，15时到家，根据这个函数图象，请你回答下列问题：
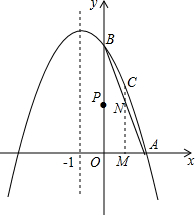如图，已知抛物线经过A（1，0），B（0，3）两点，对称轴是x=-1．