题目内容
(2011•金山区一模)已知边长为4的正方形ABCD截去一个角后成为五边形ABCFE(如图).其中EF=
,cot∠DEF=
.
(1)求线段DE、DF的长;
(2)若点P是线段EF上的一个动点,过P作PG⊥AB,PH⊥BC,设PG=x,四边形BHPG的面积y,求y关于x的函数关系式(写出定义域).并画出函数大致图象;
(3)当点P运动到四边形BHPG相邻两边之比为2:3时,求四边形BHPG的面积.

| 5 |
| 1 |
| 2 |
(1)求线段DE、DF的长;
(2)若点P是线段EF上的一个动点,过P作PG⊥AB,PH⊥BC,设PG=x,四边形BHPG的面积y,求y关于x的函数关系式(写出定义域).并画出函数大致图象;
(3)当点P运动到四边形BHPG相邻两边之比为2:3时,求四边形BHPG的面积.

分析:(1)根据cot∠DEF=
,可以设出DE=m.则DF=2m,然后利用勾股定理可以直接求出线段DE、DF的长;
(2)延长GP交DC于M,根据平行线分线断成比例可得
=
,设PG=x,表示出FM,PM的长,即可得到关系式;
(3)点P运动到四边形BHPG相邻两边之比为2:3,要分情况讨论,当
=
时,当
=
时,分别求出y的值.
| 1 |
| 2 |
(2)延长GP交DC于M,根据平行线分线断成比例可得
| PM |
| DE |
| FM |
| FD |
(3)点P运动到四边形BHPG相邻两边之比为2:3,要分情况讨论,当
| PG |
| PH |
| 2 |
| 3 |
| HP |
| PG |
| 2 |
| 3 |
解答: 解:(1)∵四边形ABCD是正方形,
解:(1)∵四边形ABCD是正方形,
∴∠D=90°,
设DE=m.则DF=2m,
DE2+DF2=EF2,
即;5m2=5,
∴m=1,
∴DE=1,DF=2;
(2)延长GP交DC于M,
∵PG⊥AB,PH⊥BC,
∴GP∥AD∥CB,
∴PH∥BG,
∴
=
,
∵PG=x,GM=BC=AD=4,
PM=4-x,FM=2(4-x),
∴PH=CM=CF+FM=2+2(4-x)=10-2x,
∴y=x(10-2x)=-2x 2+10x(3≤x≤4);
如图所示:
(3)当
=
时,
即
=
,
x=
(不合题意舍去),
当
=
时,
x=
,
y=
.
故四边形BHPG的面积为
.
 解:(1)∵四边形ABCD是正方形,
解:(1)∵四边形ABCD是正方形,∴∠D=90°,
设DE=m.则DF=2m,
DE2+DF2=EF2,
即;5m2=5,
∴m=1,
∴DE=1,DF=2;
(2)延长GP交DC于M,
∵PG⊥AB,PH⊥BC,
∴GP∥AD∥CB,

∴PH∥BG,
∴
| PM |
| DE |
| FM |
| FD |
∵PG=x,GM=BC=AD=4,
PM=4-x,FM=2(4-x),
∴PH=CM=CF+FM=2+2(4-x)=10-2x,
∴y=x(10-2x)=-2x 2+10x(3≤x≤4);
如图所示:
(3)当
| PG |
| PH |
| 2 |
| 3 |
即
| x |
| 10-2x |
| 2 |
| 3 |
x=
| 20 |
| 7 |
当
| HP |
| PG |
| 2 |
| 3 |
x=
| 15 |
| 4 |
y=
| 75 |
| 8 |
故四边形BHPG的面积为
| 75 |
| 8 |
点评:此题主要考查了勾股定理,正方形的性质,平行线分线段成比例定理,综合性较强,关键是设线段的长,利用相似的性质表示矩形的面积,用二次函数的方法解题.

练习册系列答案
 一课一练课时达标系列答案
一课一练课时达标系列答案
相关题目
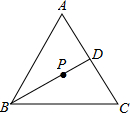 (2011•金山区一模)如图,已知:点P是等边△ABC的重心,PD=2,那么AB=
(2011•金山区一模)如图,已知:点P是等边△ABC的重心,PD=2,那么AB=