题目内容
（2011•金山区一模）若
=
，
=-4
，且|
|=|
|，则四边形ABCD是（ ）
| AB |
| e |
| CD |
| e |
| AD |
| BC |
分析：根据平面向量的几何意义，可以由
=
，
=-4
推知AB∥CD且不相等；然后根据已知条件|
|=|
|知AD、BC是四边形ABCD的两条相等的边；据此推断该四边形的形状．
| AB |
| e |
| CD |
| e |
| AD |
| BC |
解答：
解：∵
=
，
=-4
，
∴AB∥CD，且AB=4CD；
又∵|
|=|
|，
∴四边形ABCD是等腰梯形．
故选C．
解：∵| AB |
| e |
| CD |
| e |
∴AB∥CD，且AB=4CD；
又∵|
| AD |
| BC |
∴四边形ABCD是等腰梯形．
故选C．
点评：本题考查了平面向量的几何意义．解答该题的关键是根据已知条件
=
，
=-4
来判断AB与CD的方向和长度，从而确定它们的位置关系．
| AB |
| e |
| CD |
| e |
练习册系列答案
英语小英雄天天默写系列答案
暑假作业安徽少年儿童出版社系列答案
相关题目
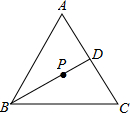（2011•金山区一模）如图，已知：点P是等边△ABC的重心，PD=2，那么AB=