题目内容
13. 如图,已知扇形AOB中,∠AOB=120°,弦AB=2$\sqrt{3}$,点M是弧AB上任意一点(与端点A、B不重合),ME⊥AB于点E,以点M为圆心、ME长为半径作⊙M,分别过点A、B作⊙M的切线,两切线相交于点C.
如图,已知扇形AOB中,∠AOB=120°,弦AB=2$\sqrt{3}$,点M是弧AB上任意一点(与端点A、B不重合),ME⊥AB于点E,以点M为圆心、ME长为半径作⊙M,分别过点A、B作⊙M的切线,两切线相交于点C.(1)求弧AB的长;
(2)试判断∠ACB的大小是否随点M的运动而改变?若不变,请求出∠ACB的大小;若改变,请说明理由.
分析 (1)过点O作OH⊥AB于H,则AH=$\frac{1}{2}$AB=$\sqrt{3}$,根据弧长公式求出结果;
(2)连接AM、BM,根据切线的判定和性质定理推出⊙M是△ABC的内切圆,得到AM、BM是∠CAB、∠ABC的平分线,求出∠AMB=90°+$\frac{1}{2}$∠ACB,由已知条件∠AOB=120,可求得∠AMB=120°,得到∠ACB=60°,求出结果.
解答 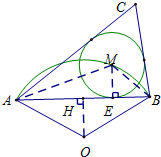 解:(1)过点O作OH⊥AB于H,
解:(1)过点O作OH⊥AB于H,
则AH=$\frac{1}{2}$AB=$\sqrt{3}$,
易求AO=2,
∴弧AB的长=$\frac{120π•2}{180}$=$\frac{4π}{3}$,
(2)连接AM、BM,
∵ME⊥AB,
∴AB是⊙M的切线,
∵AC、BC是⊙M的切线,
∴⊙M是△ABC的内切圆,
∵AM、BM是∠CAB、∠ABC的平分线,
∴∠AMB=90°+$\frac{1}{2}$∠ACB,
∵∠AOB=120°,
∴∠AMB=120°,
∴∠ACB=60°,
即∠ACB的大小不变,为60°.
点评 本题考查了等腰三角形的性质,弧长的公式,切线的判定和性质,三角形的中位线内切圆的性质,解题的关键是正确的作出辅助线.

练习册系列答案
 名校课堂系列答案
名校课堂系列答案
相关题目
1.$\sqrt{81}$的平方根是( )
| A. | 9 | B. | 3 | C. | ±9 | D. | ±3 |
8.在-3.14、$\sqrt{2}$、0,π、$\sqrt{16}$,0.101001…中,无理数的个数有( )
| A. | 3个 | B. | 2个 | C. | 1个 | D. | 4个 |
18.下列说法正确的是( )
| A. | -1的平方根是-1 | |
| B. | 任何一个非负数的立方根都是非负数 | |
| C. | 如果一个数有平方根,那么这个数的平方根一定有两个 | |
| D. | 4的平方根是2 |
5.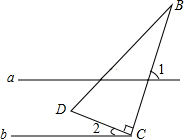 如图,直线a,b,a∥b,点C在直线b上,∠DCB=90°,若∠1=70°,则∠2的度数为( )
如图,直线a,b,a∥b,点C在直线b上,∠DCB=90°,若∠1=70°,则∠2的度数为( )
 如图,直线a,b,a∥b,点C在直线b上,∠DCB=90°,若∠1=70°,则∠2的度数为( )
如图,直线a,b,a∥b,点C在直线b上,∠DCB=90°,若∠1=70°,则∠2的度数为( )| A. | 20° | B. | 25° | C. | 30° | D. | 40° |
2.$\frac{2}{3}$的倒数是( )
| A. | $-\frac{2}{3}$ | B. | $\frac{2}{3}$ | C. | $-\frac{3}{2}$ | D. | $\frac{3}{2}$ |
 如图,∠1=100°,∠2=100°,∠3=110°,求∠4的度数.
如图,∠1=100°,∠2=100°,∠3=110°,求∠4的度数. 如图,已知直线y=$\frac{1}{2}$x与双曲线y=$\frac{k}{x}$(k>0)交于两点,且点A的横坐标为2,
如图,已知直线y=$\frac{1}{2}$x与双曲线y=$\frac{k}{x}$(k>0)交于两点,且点A的横坐标为2,