题目内容
已知：⊙O的直径AB和弦CD，且AB⊥CD于E，F为DC延长线上一点，连接AF交⊙O于M．求证：∠AMD=∠FMC．
证明：连接AD，
∵⊙O的直径AB和弦CD，且AB⊥CD，
∴弧AC=弧AD，
∴∠AMD=∠ADC，
∵A、M、C、D四点共圆，
∴∠FMC=∠ADC（圆内接四边形的一个外角等于它的内对角），
∴∠AMD=∠FMC．
分析：连接AD，根据垂径定理求出弧AD=弧AC，根据圆周角定理求出∠AMD=∠ADC，根据四点共圆求出∠FMC=∠ADC，即可推出答案．
点评：本题考查了垂径定理，圆周角定理，圆内接四边形的性质等知识点的应用，关键是作辅助线得出∠ADC=∠AMC，通过做此题培养了学生运用定理进行推理的能力．
∵⊙O的直径AB和弦CD，且AB⊥CD，
∴弧AC=弧AD，
∴∠AMD=∠ADC，
∵A、M、C、D四点共圆，
∴∠FMC=∠ADC（圆内接四边形的一个外角等于它的内对角），
∴∠AMD=∠FMC．
分析：连接AD，根据垂径定理求出弧AD=弧AC，根据圆周角定理求出∠AMD=∠ADC，根据四点共圆求出∠FMC=∠ADC，即可推出答案．
点评：本题考查了垂径定理，圆周角定理，圆内接四边形的性质等知识点的应用，关键是作辅助线得出∠ADC=∠AMC，通过做此题培养了学生运用定理进行推理的能力．
练习册系列答案
相关题目
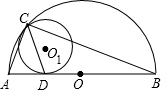如图，已知半圆O的直径AB=10，⊙O1与半圆O内切干点C，与AB相切干点D，
如图，已知半圆O的直径AB=6，点C、D是半圆的两个三等份点，则弦BC、BD和弧
如图，已知圆O的直径AB垂直于弦CD于点E，连接CO并延长交AD于点F，且CF⊥AD．
已知：⊙O的直径AB和弦CD，且AB⊥CD于E，F为DC延长线上一点，连接AF交⊙O于M．求证：∠AMD=∠FMC．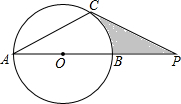
如图，已知：⊙O的直径AB与弦AC的夹角∠A=30°，过点C作⊙O的切线交AB的延长线于点P．