题目内容
 23、如图所示,已知P是正方形ABCD内一点,PA=1,PB=2,PC=3,以点B为旋转中心,将△ABP顺时针方向旋转,使点A与点C重合,这时P点旋转到G点,
23、如图所示,已知P是正方形ABCD内一点,PA=1,PB=2,PC=3,以点B为旋转中心,将△ABP顺时针方向旋转,使点A与点C重合,这时P点旋转到G点,(1)请画出旋转后的图形,你能说出此时△ABP以点B为旋转中心转了多少度吗?
(2)求证:△PGC是直角三角形.
分析:(1)根据旋转中心,旋转方向,旋转后的位置,画出图形,求出旋转角度数;
(2)由旋转的性质可得可得:△ABP≌△CBG,旋转角∠PBG=90°,BP=BG=2,先求PG,在△PCG中,已知PC=3,CG=AP=1,利用勾股定理的逆定理证明△PGC是直角三角形.
(2)由旋转的性质可得可得:△ABP≌△CBG,旋转角∠PBG=90°,BP=BG=2,先求PG,在△PCG中,已知PC=3,CG=AP=1,利用勾股定理的逆定理证明△PGC是直角三角形.
解答: (1)解:图形如下,旋转角为90°;
(1)解:图形如下,旋转角为90°;
(2)证明:由已知可得:△ABP≌△CBG,
∴BP=BG,∠ABP=∠CBG,
CG=AP=1,
又在正方形ABCD中,
∠ABC=90°,
即∠ABP+∠PBC=90°,
∴∠CBG+∠PBC=90°,
∴∠PBG=90°,
∴在Rt△PBG中,PG2=BP2+BG2=8,
又∵GC2=12=1,PC2=32=9,
∴PC2=PG2+GC2,
∴△PGC是直角三角形.
 (1)解:图形如下,旋转角为90°;
(1)解:图形如下,旋转角为90°;(2)证明:由已知可得:△ABP≌△CBG,
∴BP=BG,∠ABP=∠CBG,
CG=AP=1,
又在正方形ABCD中,
∠ABC=90°,
即∠ABP+∠PBC=90°,
∴∠CBG+∠PBC=90°,
∴∠PBG=90°,
∴在Rt△PBG中,PG2=BP2+BG2=8,
又∵GC2=12=1,PC2=32=9,
∴PC2=PG2+GC2,
∴△PGC是直角三角形.
点评:本题考查旋转的性质--旋转变化前后,对应线段、对应角分别相等,图形的大小、形状都不改变;以及勾股定理的逆定理的运用.

练习册系列答案
 名师伴你成长课时同步学练测系列答案
名师伴你成长课时同步学练测系列答案
相关题目
 三角形?若存在,求出点C的坐标,并证明;若不存在,请说明理由.
三角形?若存在,求出点C的坐标,并证明;若不存在,请说明理由. 色花,第二层摆黄色花,第三层是紫色花,第四层摆红色花…由里向外依次按红、黄、紫的颜色摆放.
色花,第二层摆黄色花,第三层是紫色花,第四层摆红色花…由里向外依次按红、黄、紫的颜色摆放.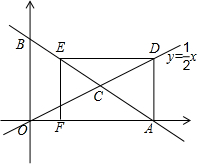 如图所示,已知A点的坐标为(6,0),B是y轴正半轴上的一动点,直线AB交直线
如图所示,已知A点的坐标为(6,0),B是y轴正半轴上的一动点,直线AB交直线 如图所示,已知边长为a的等边三角形ABC,两顶点A,分别在x轴,y轴的正半轴上滑动,连接OC,则OC长的最大值是
如图所示,已知边长为a的等边三角形ABC,两顶点A,分别在x轴,y轴的正半轴上滑动,连接OC,则OC长的最大值是 数学家高斯在读小学二年级时,老师给出了这样一道题:1+2+3+…+100=?高斯很快做出了答案,他的计算方法是:1+2+3+…+100=(1+100)+(2+99)+(3+98)+…+(50+51)=50×101=5 050.根据此方法,试探究:有一堆堆放整齐的钢管其主(正)视图如图所示,已知最下面一层有钢管50根,最上面一层有4根,则共有钢管
数学家高斯在读小学二年级时,老师给出了这样一道题:1+2+3+…+100=?高斯很快做出了答案,他的计算方法是:1+2+3+…+100=(1+100)+(2+99)+(3+98)+…+(50+51)=50×101=5 050.根据此方法,试探究:有一堆堆放整齐的钢管其主(正)视图如图所示,已知最下面一层有钢管50根,最上面一层有4根,则共有钢管