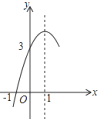Question

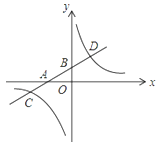
【题目】如图直线y＝kx+k交x轴负半轴于点A，交y轴正半轴于点B，且AB＝2

（1）求k的值；

（2）点P从A出发，以每秒1个单位的速度沿射线AB运动，过点P作直线AB的垂线交x轴于点Q，连接OP，设△PQO的面积为S，点P运动时间为t，求S与t的函数关系式，并直接写出t的取值范围；

（3）在（2）的条件下，当P在AB的延长线上，若OQ+AB＝（BQ﹣OP），求此时直线PQ的解析式．

Answer 1

【答案】（1）k＝．（2）当0＜t＜时，S＝OQPy＝（1﹣2t）t＝﹣t2+t．

当t＞时，S＝OQPy＝（2t﹣1）t＝t2﹣t．（3）直线PQ的解析式为y＝﹣x+．

【解析】

（1）求出点B的坐标即可解决问题；（2）分两种情形①当0＜t＜时，②当t＞时，根据S＝OQPy，分别求解即可；（3）根据已知条件构建方程求出t，推出点P，Q的坐标即可解决问题．

解：（1）对于直线y＝kx+k，令y＝0，可得x＝﹣1，

∴A（﹣1，0），

∴OA＝1，∵AB＝2，

∴OB＝

∴k＝．

（2）如图，

∵tan∠BAO＝

∴∠BAO＝60°，

∵PQ⊥AB，

∴∠APQ＝90°，

∴∠AQP＝30°，

∴AQ＝2AP＝2t，

当0＜t＜时，S＝OQPy＝（1﹣2t）t＝﹣t2+t．

当t＞时，S＝OQPy＝（2t﹣1）t＝t2﹣t．

（3）∵OQ+AB＝（BQ﹣OP），

∴2t﹣1+2＝

∴2t+1＝

∴4t2+4t+1＝7t2﹣7t+7，

∴3t2﹣11t+6＝0，

解得t＝3或（舍弃），

∴P（，），Q（5，0），

设直线PQ的解析式为y＝kx+b，则有，

解得 ，

∴直线PQ的解析式为．