题目内容
5. 如图,四边形ABCD是长方形(长方形对边相等且平行,四个角为直角),
如图,四边形ABCD是长方形(长方形对边相等且平行,四个角为直角),(1)用直尺和圆规在边CD上找一个点P,使△ADP沿着直线AP翻折后D点正好落在BC边上的Q点(不写作法,保留作图痕迹).连结AP,AQ,PQ;
(2)在(1)中作的新图形中,已知AB=5,AD=13,求CP的长.
分析 (1)以A为圆心,以AD为半径交BC于点Q,作出∠DAQ的平分线,交CD于点P;
(2)利用△ABQ∽△QCP,根据相似三角形的对应边的比相等求得CP的值.
解答 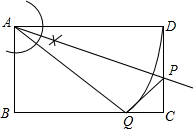 解:(1)点P就是所求的图形;
解:(1)点P就是所求的图形;
(2)在直角△ABQ中,BQ=$\sqrt{A{Q}^{2}-A{B}^{2}}$=$\sqrt{1{3}^{2}-{5}^{2}}$=12,
则QC=BC-BQ=13-12=1,
∵∠AQP=∠ADC=90°,
∴∠AQB+∠PQC=90°,
又∵直角△ABQ中,∠BAQ+∠AQP=90°,
∴∠PQC=∠BAQ,
又∵∠B=∠C=90°,
∴△ABQ∽△QCP,
∴$\frac{CP}{BQ}$=$\frac{QC}{AB}$,即$\frac{CP}{12}$=$\frac{1}{5}$,
解得:CP=$\frac{12}{5}$.
点评 本题考查了矩形的性质以及相似三角形的判定与性质,正确应用相似三角形的判定与性质是解题关键.

练习册系列答案
相关题目
20.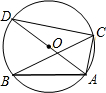 如图,△ABC内接于圆O,AD是圆O的直径,∠ABC=30°,则∠CAD的度数等于( )
如图,△ABC内接于圆O,AD是圆O的直径,∠ABC=30°,则∠CAD的度数等于( )
 如图,△ABC内接于圆O,AD是圆O的直径,∠ABC=30°,则∠CAD的度数等于( )
如图,△ABC内接于圆O,AD是圆O的直径,∠ABC=30°,则∠CAD的度数等于( )| A. | 45° | B. | 50° | C. | 55° | D. | 60° |
14.下列计算正确的是( )
| A. | 3x2y-3x2y=0 | B. | 3x2+2x2=5x4 | C. | 3x2-2x2=1 | D. | 3x+2y=5xy |
