题目内容
 如图,在△ABC中,CD⊥AB,垂足为D,点E在BC上,EF⊥AB,垂足为F.
如图,在△ABC中,CD⊥AB,垂足为D,点E在BC上,EF⊥AB,垂足为F.(1)CD与EF平行吗?为什么?
(2)如果∠1=∠2,且∠3=120°,求∠ACB的度数.
考点:平行线的判定与性质
专题:
分析:(1)根据垂直定义得出∠EFB=∠CDB=90°,根据平行线的判定得出即可;
(2)根据平行线的性质和已知求出∠1=∠2=∠DCB,推出DG∥BC,根据平行线的性质得出即可.
(2)根据平行线的性质和已知求出∠1=∠2=∠DCB,推出DG∥BC,根据平行线的性质得出即可.
解答:解:(1)CD∥EF,
理由是:∵CD⊥AB,EF⊥AB,
∴∠EFB=∠CDB=90°,
∴CD∥EF;
(2)∵CD∥EF,
∴∠2=∠DCB,
∵∠1=∠2,
∴∠1=∠DCB,
∴DG∥BC,
∴∠ACB=∠3,
∵∠3=120°,
∴∠ACB=120°.
理由是:∵CD⊥AB,EF⊥AB,
∴∠EFB=∠CDB=90°,
∴CD∥EF;
(2)∵CD∥EF,
∴∠2=∠DCB,
∵∠1=∠2,
∴∠1=∠DCB,
∴DG∥BC,
∴∠ACB=∠3,
∵∠3=120°,
∴∠ACB=120°.
点评:本题考查了对平行线的性质和判定的应用,注意:平行线的性质是①两直线平行,同位角相等,②两直线平行,内错角相等,③两直线平行,同旁内角互补,反之亦然.

练习册系列答案
 超能学典应用题题卡系列答案
超能学典应用题题卡系列答案
相关题目
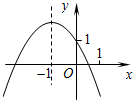 已知二次函数y=ax2+bx+c的图象如图所示,有以下结论.其中,错误的结论是( )
已知二次函数y=ax2+bx+c的图象如图所示,有以下结论.其中,错误的结论是( )| A、abc>0 | ||
| B、a+b<-1 | ||
C、2a-b<-
| ||
| D、c-a>1 |
-6
根号外的因式移到根号内的结果为( )
|
A、-
| ||
B、
| ||
C、-
| ||
D、
|
 如图,梯形ABCD的两条对角线交于点E,图中面积相等的三角形共有
如图,梯形ABCD的两条对角线交于点E,图中面积相等的三角形共有 如图,如果∠3+∠4=180°,那么∠1与∠2是否相等?为什么?
如图,如果∠3+∠4=180°,那么∠1与∠2是否相等?为什么? 如图,已知AD平分∠BAC,要使△ABD≌△ACD,
如图,已知AD平分∠BAC,要使△ABD≌△ACD,