题目内容
 如图,⊙O1、⊙O2内切于P点,连心线和⊙O1、⊙O2分别交于A、B两点,过P点的直线与⊙O1、⊙O2分别交于C、D两点,若∠BPC=60°,AB=2,则CD=
如图,⊙O1、⊙O2内切于P点,连心线和⊙O1、⊙O2分别交于A、B两点,过P点的直线与⊙O1、⊙O2分别交于C、D两点,若∠BPC=60°,AB=2,则CD=
- A.1
- B.2
- C.

- D.

A
分析:根据相切两圆的性质得出相切两圆连心线必过切点,以及利用解直角三角形的知识求出 PA+1=
PA+1= PA+CD,从而求出即可.
PA+CD,从而求出即可.
解答: 解:连接AC,BD,
解:连接AC,BD,
∵⊙O1、⊙O2内切于P点,连心线和⊙O1、⊙O2分别交于A、B两点,
∴PA是⊙O1直径,PB是⊙O2直径,
∴∠PCA=∠PDB=90°,
∵∠BPC=60°,AB=2,
∴PC= PA,PD=
PA,PD= PB=
PB= (PA+2)=PC+CD=
(PA+2)=PC+CD= PA+CD,
PA+CD,
∴ PA+1=
PA+1= PA+CD,
PA+CD,
∴CD=1.
故选:A.
点评:此题主要考查了相切两圆的性质已积解直角三角新,利用其性质得出∠PCA=∠PDB=90°,进而求出PD= PB=
PB= (PA+2)=PC+CD=
(PA+2)=PC+CD= PA+CD是解题关键.
PA+CD是解题关键.
分析:根据相切两圆的性质得出相切两圆连心线必过切点,以及利用解直角三角形的知识求出
 PA+1=
PA+1= PA+CD,从而求出即可.
PA+CD,从而求出即可.解答:
 解:连接AC,BD,
解:连接AC,BD,∵⊙O1、⊙O2内切于P点,连心线和⊙O1、⊙O2分别交于A、B两点,
∴PA是⊙O1直径,PB是⊙O2直径,
∴∠PCA=∠PDB=90°,
∵∠BPC=60°,AB=2,
∴PC=
 PA,PD=
PA,PD= PB=
PB= (PA+2)=PC+CD=
(PA+2)=PC+CD= PA+CD,
PA+CD,∴
 PA+1=
PA+1= PA+CD,
PA+CD,∴CD=1.
故选:A.
点评:此题主要考查了相切两圆的性质已积解直角三角新,利用其性质得出∠PCA=∠PDB=90°,进而求出PD=
 PB=
PB= (PA+2)=PC+CD=
(PA+2)=PC+CD= PA+CD是解题关键.
PA+CD是解题关键. 
练习册系列答案
相关题目
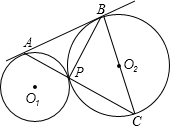 如图,⊙O1与⊙O2外切于点P,外公切线AB切⊙O1于点A,切⊙O2于点B,
如图,⊙O1与⊙O2外切于点P,外公切线AB切⊙O1于点A,切⊙O2于点B,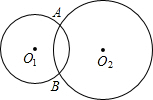 如图,⊙O1、⊙O2相交于点A、B,现给出4个命题:
如图,⊙O1、⊙O2相交于点A、B,现给出4个命题: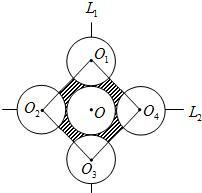 如图,⊙O1,⊙O2,⊙O3,⊙O4,⊙O的半径均为2cm,⊙O与⊙O1,⊙O3相外切,⊙O与⊙O2,⊙O4相外切,并且圆心分别位于两条互相垂直的直线L1,L2上,连接O1,O2,O3,O4得四边形O1O2O3O4,则图中阴影部分的面积为
如图,⊙O1,⊙O2,⊙O3,⊙O4,⊙O的半径均为2cm,⊙O与⊙O1,⊙O3相外切,⊙O与⊙O2,⊙O4相外切,并且圆心分别位于两条互相垂直的直线L1,L2上,连接O1,O2,O3,O4得四边形O1O2O3O4,则图中阴影部分的面积为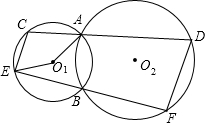 已知:如图,⊙O1和⊙O2相交于A、B两点,经过A的直线CD与⊙O1交于点C、与⊙O2交于点D,经过点B的直线EF与⊙O1交于点E、与⊙O2交于点F,连接CE、DF.若∠AO1E=100°,则∠D的度数为
已知:如图,⊙O1和⊙O2相交于A、B两点,经过A的直线CD与⊙O1交于点C、与⊙O2交于点D,经过点B的直线EF与⊙O1交于点E、与⊙O2交于点F,连接CE、DF.若∠AO1E=100°,则∠D的度数为 (1998•南京)如图,⊙O1和⊙O2内切于点P,⊙O2的弦AB经过⊙O1的圆心O1,交⊙O1于点C、D,若AC:CD:BD=3:4:2,则⊙O1与⊙O2的直径之比为( )
(1998•南京)如图,⊙O1和⊙O2内切于点P,⊙O2的弦AB经过⊙O1的圆心O1,交⊙O1于点C、D,若AC:CD:BD=3:4:2,则⊙O1与⊙O2的直径之比为( )