题目内容
9.在平面直角坐标系中,横、纵坐标都是整数的点叫做“整点”,例如点(0,0),(1,2),(-2,5)等,请写出一个在函数y=$\frac{1}{4}$x-$\frac{1}{2}$图象上的“整点”(-2,0).分析 若满足函数y=$\frac{1}{4}$x-$\frac{1}{2}$图象上的整点,则x=4y-2,将y整数代入可求得整点.
解答 解:由y=$\frac{1}{4}$x-$\frac{1}{2}$得x=4y-2,且y为整数,
则将y整数代入可求得整点,如(-2,0);
故答案为(-2,0).
点评 本题考查了一次函数图象上点的坐标特征,把y=$\frac{1}{4}$x-$\frac{1}{2}$变形得x=4y-2是解题的关键.

练习册系列答案
 培优好卷单元加期末卷系列答案
培优好卷单元加期末卷系列答案 一线名师权威作业本系列答案
一线名师权威作业本系列答案
相关题目
19.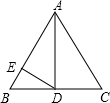 如图,在等边△ABC中,AD是BC边的中线,DE⊥AB,垂足为E,等边△ABC边长是6cm,则BE长为( )
如图,在等边△ABC中,AD是BC边的中线,DE⊥AB,垂足为E,等边△ABC边长是6cm,则BE长为( )
 如图,在等边△ABC中,AD是BC边的中线,DE⊥AB,垂足为E,等边△ABC边长是6cm,则BE长为( )
如图,在等边△ABC中,AD是BC边的中线,DE⊥AB,垂足为E,等边△ABC边长是6cm,则BE长为( )| A. | 1cm | B. | 1.5cm | C. | 2cm | D. | 2.5cm |
20.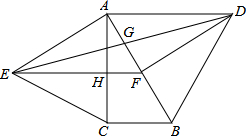 如图,分别以直角△ABC的斜边AB,直角边AC为边向△ABC外作等边△ABD和等边△ACE,F为AB的中点,DE与AB交于点G,EF与AC交于点H,∠ACB=90°,∠BAC=30°,下列结论不正确的是( )
如图,分别以直角△ABC的斜边AB,直角边AC为边向△ABC外作等边△ABD和等边△ACE,F为AB的中点,DE与AB交于点G,EF与AC交于点H,∠ACB=90°,∠BAC=30°,下列结论不正确的是( )
 如图,分别以直角△ABC的斜边AB,直角边AC为边向△ABC外作等边△ABD和等边△ACE,F为AB的中点,DE与AB交于点G,EF与AC交于点H,∠ACB=90°,∠BAC=30°,下列结论不正确的是( )
如图,分别以直角△ABC的斜边AB,直角边AC为边向△ABC外作等边△ABD和等边△ACE,F为AB的中点,DE与AB交于点G,EF与AC交于点H,∠ACB=90°,∠BAC=30°,下列结论不正确的是( )| A. | EF⊥AC | B. | AD=4AG | ||
| C. | 四边形ADEF为菱形 | D. | FH=$\frac{1}{4}$BD |
4.下列各组数据中不能构成直角三角形的一组数据是( )
| A. | 4-$\sqrt{3}$,4+$\sqrt{3}$,$\sqrt{38}$ | B. | $\frac{5}{4}$,$\frac{3}{4}$,1 | ||
| C. | k,2k,$\sqrt{3}$k | D. | 2m2+1,2m2-1,2m(m是大于1的整数) |
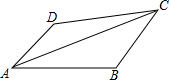 在四边形ABCD中,∠DAB=∠DCB=45°,AD=$3\sqrt{2}$,DC=$5\sqrt{2}$,AB=7,则对角线AC的长为$2\sqrt{29}$.
在四边形ABCD中,∠DAB=∠DCB=45°,AD=$3\sqrt{2}$,DC=$5\sqrt{2}$,AB=7,则对角线AC的长为$2\sqrt{29}$.