题目内容
17.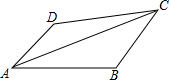 在四边形ABCD中,∠DAB=∠DCB=45°,AD=$3\sqrt{2}$,DC=$5\sqrt{2}$,AB=7,则对角线AC的长为$2\sqrt{29}$.
在四边形ABCD中,∠DAB=∠DCB=45°,AD=$3\sqrt{2}$,DC=$5\sqrt{2}$,AB=7,则对角线AC的长为$2\sqrt{29}$.
分析 过D,C点作DE⊥AB,CF⊥AB,根据勾股定理得出AE和DE的长度,再得出BE的长度,得出DB的长度,进而得出CB和CF,最后利用勾股求出AC的长度.
解答 解:过D,C点作DE⊥AB,CF⊥AB,连接DB,如图: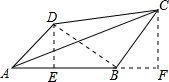
∵∠DAB=45°,DE⊥AB,AD=$3\sqrt{2}$,
∴AE=3,DE=3,
∵AB=7,
∴BE=4,
∴DB=$\sqrt{{3}^{2}+{4}^{2}}=5$,
∵∠DCB=45°,DC=$5\sqrt{2}$,DB=5,
∴BC=5,
∵∠EBD+∠CBF=90°,∠CDF+∠FCB=90°,
∴∠EBD=∠FCB,
在△DEB和△BFC中,
$\left\{\begin{array}{l}{∠DEB=∠BFC}\\{∠EBD=∠FCB}\\{DB=BC}\end{array}\right.$,
∴△DEB≌△BFC(AAS),
∴BF=DE=3,CF=BE=4,
∴AF=7+3=10,
在Rt△ACF中,
AC=$\sqrt{1{0}^{2}+{4}^{2}}=2\sqrt{29}$.
故答案为:$2\sqrt{29}$.
点评 此题考查全等三角形的判定和性质,关键是构建全等三角形,同时运用勾股定理进行计算.

练习册系列答案
 阅读快车系列答案
阅读快车系列答案
相关题目
5.下列命题中,正确的是( )
| A. | 平分弦的直线必垂直于这条弦 | |
| B. | 垂直平分弦的直线必平分这条弦所对的弧 | |
| C. | 平分弦的直径必垂直于这条弦,并且平分这条弦所对的两条弧 | |
| D. | 垂直于弦的直线必过圆心 |
12.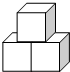 如图的几何体是由三个同样大小的立方体搭成的,则下列说法正确的是( )
如图的几何体是由三个同样大小的立方体搭成的,则下列说法正确的是( )
 如图的几何体是由三个同样大小的立方体搭成的,则下列说法正确的是( )
如图的几何体是由三个同样大小的立方体搭成的,则下列说法正确的是( )| A. | 主视图的面积最大 | B. | 左视图的面积最大 | ||
| C. | 俯视图的面积最大 | D. | 三个视图的面积一样大 |
6.下列说法中错误的是( )
| A. | 某种彩票的中奖率为1%,买100张彩票也可能没有1张的是中奖 | |
| B. | 从装有10个红球的袋子中,摸出1个白球是不可能事件 | |
| C. | 陨石落在地球上,它会落入海洋的概率是$\frac{1}{2}$ | |
| D. | 在13位同学中,一定有2位同学的出生月份是相同的 |
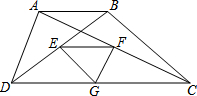 如图,梯形ABCD中,AB∥CD,点E、F、G分别是BD、AC、DC的中点.已知两底差是6,两腰和是12,则△EFG的周长是9.
如图,梯形ABCD中,AB∥CD,点E、F、G分别是BD、AC、DC的中点.已知两底差是6,两腰和是12,则△EFG的周长是9. 如图,在矩形ABCD中,AD=$\sqrt{2}$AB,∠BAD的平分线交BC于点E,DH⊥AE于点H,连接BH并延长交CD于点F,连接DE交BF于点O,下列结论:
如图,在矩形ABCD中,AD=$\sqrt{2}$AB,∠BAD的平分线交BC于点E,DH⊥AE于点H,连接BH并延长交CD于点F,连接DE交BF于点O,下列结论: 如图,AB∥CD,∠1=112°,则∠C=68°.
如图,AB∥CD,∠1=112°,则∠C=68°.