题目内容
如图17，在Rt△ABC中，∠ACB=90°，AC=AE，BC=BD，则∠ACD+∠BCE=______．
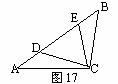
．解一：如图25，设∠ACD=∠1，∠BCE=∠2，∠DCE=∠3．∵AC=AE，∴∠AEC=∠1+∠3．
∵BC=BD，∴∠BDC=∠2+∠3．
两式相加得∠AEC+∠BDC=(∠1+∠2+∠3)+∠3=90°+∠3．
又在△DCE中∠DEC+∠EDC+∠3=180°．∴90°+2∠3=180°,∠3=45°，∴∠1+∠2=45°．
解二：∵∠ACE是等腰△ACE的底角，∴
练习册系列答案
天天向上一本好卷系列答案
小学生10分钟应用题系列答案
相关题目
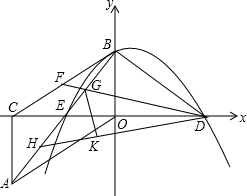O沿y轴对折得到Rt△BDO．取BC中点F，连接DF，交AB于点G，将△BDG沿DF对折得到△KDG．直线DK交AB于点H．
如图：已知M是Rt△ABC的斜边BC的中点，P、Q分别在AB、AC上且BP=5，CQ=3，PM⊥QM，则PQ为（ ）
