题目内容
 如图:已知M是Rt△ABC的斜边BC的中点,P、Q分别在AB、AC上且BP=5,CQ=3,PM⊥QM,则PQ为( )
如图:已知M是Rt△ABC的斜边BC的中点,P、Q分别在AB、AC上且BP=5,CQ=3,PM⊥QM,则PQ为( )分析:延长QM至D,是DM=QM,连接BD、PD,然后利用“边角边”证明△CMQ和△BMD全等,根据全等三角形对应边相等可得BD=CQ,全等三角形对应角相等可得∠DBM=∠C,然后求出∠PBD=90°,再根据线段垂直平分线上的点到线段两端点的距离相等可得PD=PQ,然后利用勾股定理列式进行计算即可得解.
解答: 解:延长QM至D,使DM=QM,连接BD、PD,
解:延长QM至D,使DM=QM,连接BD、PD,
∵M是边BC的中点,
∴BM=CM,
在△CMQ和△BMD中,
∵
,
∴△CMQ≌△BMD(SAS),
∴BD=CQ,∠DBM=∠C,
在△ABC中,∵∠A=90°,
∴∠C+∠ABC=90°,
∴∠DBM+∠ABC=90°,
即∠PBD=90°,
又∵PM⊥QM,DM=QM,
∴PD=PQ,
∵BP=5,CQ=3,
∴在Rt△PBD中,根据勾股定理,PD=
=
=
,即PQ=
.
故选C.
 解:延长QM至D,使DM=QM,连接BD、PD,
解:延长QM至D,使DM=QM,连接BD、PD,∵M是边BC的中点,
∴BM=CM,
在△CMQ和△BMD中,
∵
|
∴△CMQ≌△BMD(SAS),
∴BD=CQ,∠DBM=∠C,
在△ABC中,∵∠A=90°,
∴∠C+∠ABC=90°,
∴∠DBM+∠ABC=90°,
即∠PBD=90°,
又∵PM⊥QM,DM=QM,
∴PD=PQ,
∵BP=5,CQ=3,
∴在Rt△PBD中,根据勾股定理,PD=
| PB2+BD2 |
| 52+32 |
| 34 |
| 34 |
故选C.
点评:本题考查了全等三角形的判定与性质,勾股定理的应用,作辅助线,构造出全等三角形与直角三角形是解题的关键,也是本题的难点.

练习册系列答案
 中考解读考点精练系列答案
中考解读考点精练系列答案 各地期末复习特训卷系列答案
各地期末复习特训卷系列答案 小博士期末闯关100分系列答案
小博士期末闯关100分系列答案
相关题目
 如图,已知M是Rt△ABC斜边AB的中点,CD=BM,DM与CB的延长线交于点E.
如图,已知M是Rt△ABC斜边AB的中点,CD=BM,DM与CB的延长线交于点E.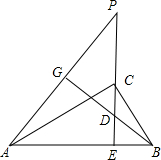 如图,已知CE是Rt△ABC斜边AB上的高,在EC的延长线上任取一点P,连接AP,BG⊥AP垂足为G,交CE于D,
如图,已知CE是Rt△ABC斜边AB上的高,在EC的延长线上任取一点P,连接AP,BG⊥AP垂足为G,交CE于D, 15、如图,已知AB是Rt△ABC和Rt△ABD的斜边,O是AB的中点,其中OC是2cm,则OD=
15、如图,已知AB是Rt△ABC和Rt△ABD的斜边,O是AB的中点,其中OC是2cm,则OD= 如图,已知AD是Rt△ABC斜边BC上的高,且AB=6,BC=10.则AC=
如图,已知AD是Rt△ABC斜边BC上的高,且AB=6,BC=10.则AC=