题目内容
在Rt△ABC中,∠C=90°,以BC为直径画圆交斜边于D,过点D作⊙O的切线交AC于E.
(1)求证:∠DEC=∠B.
(2)若∠B=30°,BC=6,求切线DE的长.
(1)求证:∠DEC=∠B.
(2)若∠B=30°,BC=6,求切线DE的长.
考点:切线的性质
专题:证明题
分析:(1)根据圆周角定理,由BC是直径得到∠CDB=90°,则∠B+∠DCB=90°,再根据切线的性质得到∠ECD+∠ODC=90°,加上∠ODC=∠DCO,于是有∠EDC=∠B;
(2)先判断AC为⊙O的切线,根据切线长定理得到EC=ED,则∠EDC=∠ECD,而∠EDC=∠B,所以∠B=∠ECD=∠EDC=30°,再根据三角形外角性质可计算出∠AED=∠ECD+∠EDC=60°,易得△ADE为等边三角形,所以AE=ED,则AE=EC=DE,然后在Rt△ABC中根据含30度的直角三角形三边的关系计算出AC=
BC=2
,于是得到DE=
AC=
.
(2)先判断AC为⊙O的切线,根据切线长定理得到EC=ED,则∠EDC=∠ECD,而∠EDC=∠B,所以∠B=∠ECD=∠EDC=30°,再根据三角形外角性质可计算出∠AED=∠ECD+∠EDC=60°,易得△ADE为等边三角形,所以AE=ED,则AE=EC=DE,然后在Rt△ABC中根据含30度的直角三角形三边的关系计算出AC=
| ||
| 3 |
| 3 |
| 1 |
| 2 |
| 3 |
解答:(1)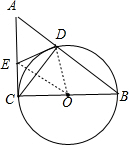 证明:∵BC是直径,
证明:∵BC是直径,
∴∠CDB=90°,
∴∠B+∠DCB=90°,
∵ED是切线,
∴OD⊥DE,
∴∠ECD+∠ODC=90°,
∵OB=OC,
∴∠ODC=∠DCO,
∴∠EDC=∠B;
(2)解:∵∠ACB=90°,BC是直径,
∴AC为⊙O的切线,
∴EC=ED,
∴∠EDC=∠ECD,
而∠EDC=∠B,
∴∠B=∠ECD=∠EDC=30°,
∴∠AED=∠ECD+∠EDC=60°,
而∠A=90°-∠B=60°,
∴△ADE为等边三角形,
∴AE=ED,
∴AE=EC=DE,
在Rt△ABC中,∵BC=6,∠B=30°
∴AC=
BC=2
,
∴DE=
AC=
.
 证明:∵BC是直径,
证明:∵BC是直径,∴∠CDB=90°,
∴∠B+∠DCB=90°,
∵ED是切线,
∴OD⊥DE,
∴∠ECD+∠ODC=90°,
∵OB=OC,
∴∠ODC=∠DCO,
∴∠EDC=∠B;
(2)解:∵∠ACB=90°,BC是直径,
∴AC为⊙O的切线,
∴EC=ED,
∴∠EDC=∠ECD,
而∠EDC=∠B,
∴∠B=∠ECD=∠EDC=30°,
∴∠AED=∠ECD+∠EDC=60°,
而∠A=90°-∠B=60°,
∴△ADE为等边三角形,
∴AE=ED,
∴AE=EC=DE,
在Rt△ABC中,∵BC=6,∠B=30°
∴AC=
| ||
| 3 |
| 3 |
∴DE=
| 1 |
| 2 |
| 3 |
点评:本题考查了切线的性质:圆的切线垂直于经过切点的半径.若出现圆的切线,必连过切点的半径,构造定理图,得出垂直关系.

练习册系列答案
 步步高达标卷系列答案
步步高达标卷系列答案
相关题目
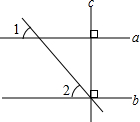 如图,直线a,b,c,d,已知c⊥a,c⊥b,直线b,c,d交于一点,若∠1=50°,
如图,直线a,b,c,d,已知c⊥a,c⊥b,直线b,c,d交于一点,若∠1=50°,则∠2的余角等于( )
| A、60° | B、50° |
| C、40° | D、30° |
下列计算正确的是( )
| A、a7÷a5=a2 |
| B、a2•a3=a6 |
| C、(-a3)2=-a6 |
| D、a+a=a2 |
 如图,∠1+∠2=220°,b∥c,则∠3=( )
如图,∠1+∠2=220°,b∥c,则∠3=( )| A、110° | B、120° |
| C、70° | D、60° |
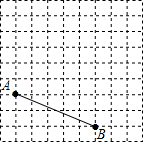 如图,方格纸中每个小正方形的边长都是1,点A、B是方格纸中的两个格点(即小正方形的顶点).
如图,方格纸中每个小正方形的边长都是1,点A、B是方格纸中的两个格点(即小正方形的顶点).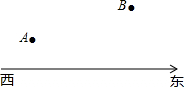 如图,两所学校位于A、B两处,且在一条东西走向公路的同旁,一辆汽车由西向东行驶,在行驶过程中是否存在一点C,使C点到A、B两校的距离相等,如果有,请用尺规作图找出该点,保留作图痕迹.
如图,两所学校位于A、B两处,且在一条东西走向公路的同旁,一辆汽车由西向东行驶,在行驶过程中是否存在一点C,使C点到A、B两校的距离相等,如果有,请用尺规作图找出该点,保留作图痕迹.