题目内容
8.如果x1、x2是一元二次方程x2-2x-8=0的两个根,那么x1+x2的值是2.分析 根据一元二次方程的根与系数的关系得到两根之和即可.
解答 解:∵方程x2-2x-8=0的两个根是x1,x2,
∴x1+x2=-(-2)=2.
故答案为:2.
点评 本题考查了一元二次方程ax2+bx+c=0的根与系数关系即韦达定理,两根之和是-$\frac{b}{a}$,两根之积是$\frac{c}{a}$.

练习册系列答案
 导学全程练创优训练系列答案
导学全程练创优训练系列答案
相关题目
6.大于-1而小于$\sqrt{15}$的整数是( )
| A. | 0、1、2、3 | B. | 1、2、3 | C. | 2、3、4 | D. | 0、1、2、3、4 |
3.下列各组线段中,成比例线段的组是( )
| A. | 3cm,4cm,5cm,8cm | B. | 1cm,3cm,4cm,8cm | ||
| C. | 2.1cm,3.2cm,5.4cm,6.5cm | D. | 0.15cm,0.18cm,4cm,4.8cm. |
17.若(a+b)2加上一个单项式后等于(a-b)2,则这个单项式为( )
| A. | 2ab | B. | -2ab | C. | 4ab | D. | -4ab |
18.下列各式中正确的是( )
| A. | ${({\frac{{2{x^2}}}{2y}})^3}=\frac{{2{x^6}}}{{2{y^3}}}$ | B. | ${({\frac{2a}{a+b}})^2}=\frac{{4{a^2}}}{{{a^2}+{b^2}}}$ | ||
| C. | ${({\frac{m+n}{m-n}})^3}=\frac{{{{(m+n)}^3}}}{{{{(m-n)}^3}}}$ | D. | ${({\frac{x-y}{x+y}})^2}=\frac{{{x^2}-{y^2}}}{{{x^2}+{y^2}}}$ |
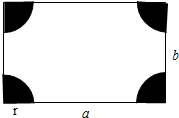 如图,在一长方形休闲广声场的四角都设计一块半径相同的四分之一圆的花坛,若圆形的半径为r米,广场的长为a米,宽为b米.
如图,在一长方形休闲广声场的四角都设计一块半径相同的四分之一圆的花坛,若圆形的半径为r米,广场的长为a米,宽为b米.