题目内容
2．
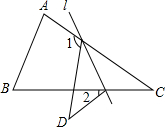如图，在△ABC中，∠C=40°，将△ABC沿着直线l折叠，点C落在点D的位置，则∠1-∠2的度数是（ ）| A． | 40° | B． | 80° | C． | 90° | D． | 140° |
分析 由折叠的性质得到∠D=∠C，再利用外角性质即可求出所求角的度数．
解答 
解：由折叠的性质得：∠D=∠C=40°，
根据外角性质得：∠1=∠3+∠C，∠3=∠2+∠D，
则∠1=∠2+∠C+∠D=∠2+2∠C=∠2+80°，
则∠1-∠2=80°．
故选B．
点评 此题考查了翻折变换（折叠问题），以及外角性质，熟练掌握折叠的性质是解本题的关键．
练习册系列答案
相关题目
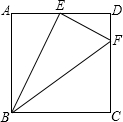在正方形ABCD中，点E为AD中点，DF=$\frac{1}{4}$CD，则下列说法：（1）BE⊥EF；（2）图中有3对相似三角形；（3）E到BF的距离为$\frac{1}{2}$AB；（4）$\frac{{S}_{△BEF}}{{S}_{△BCF}}$=$\frac{5}{7}$．其中正确的有（ ）
如图所示，∠1～∠8这8个角中，同位角、内错角、同旁内角各有几对？请分别写出来．
8．已知$\frac{x}{2}=\frac{y}{3}$，那么下列式子中一定成立的是（ ）
| A． | x+y=5 | B． | 2x=3y | C． | $\frac{x}{y}=\frac{3}{2}$ | D． | $\frac{x}{y}=\frac{2}{3}$ |
如图，在平面直角坐标系内，已知点A（0，6），点B（8，0），AB=10．动点P从点A开始在线段AO上以每秒1个单位长度的速度向点O移动，同时动点Q从点B开始在线段BA上以每秒2个单位长度的速度向点A移动，设点P、Q移动的时间为t秒．