Question

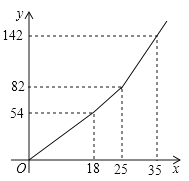
【题目】某地区年投入教育经费万元，年投入教育经费万元．

（1）求年至年该地区投入教育经费的年平均增长率；

（2）根据（1）所得的年平均增长率，预计年该地区将投入教育经费多少万元．

Answer 1

【答案】（1）10%；（2）3327.5万

【解析】

（1）一般用增长后的量=增长前的量×（1+增长率），2016年要投入教育经费是2500（1+x）万元，在2017年的基础上再增长x，就是2017年的教育经费数额，即可列出方程求解．

（2）利用（1）中求得的增长率来求2018年该地区将投入教育经费．

设增长率为x,根据题意2016年为2500(1+x)万元,2017年为2500(1+x) 万元。

则2500(1+x) =3025，

解得x=0.1=10%,或x=2.1(不合题意舍去).

答：这两年投入教育经费的平均增长率为10%.

(2)3025×(1+10%)=3327.5(万元).

故根据(1)所得的年平均增长率，预计2018年该地区将投入教育经费3327.5万.