题目内容
10.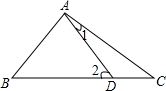 如图,已知D是BC上一点,且满足AB=AC=BD,那么∠1与∠2的关系是( )
如图,已知D是BC上一点,且满足AB=AC=BD,那么∠1与∠2的关系是( )| A. | 3∠2-∠1=180° | B. | ∠1+2∠2=180° | C. | 2∠1+∠2=180° | D. | ∠1=2∠2 |
分析 由AB=AC=BD,可得∠BAD=∠2,∠B=∠C,又由三角形的内角和定理,可得2∠C+∠2+∠1=180°,然后由三角形外角的性质,求得∠C=∠2-∠1,即可求得答案.
解答 解:∵AB=BD,
∴∠BAD=∠2,
∵AB=AC,
∴∠B=∠C,
∵∠B+∠C+∠BAC=180°,
∴2∠C+∠2+∠1=180°,
∵∠C=∠2-∠1,
∴3∠2-∠1=180°
故选A.
点评 此题主要考查学生对等腰三角形的判定与性质,三角形内角和定理,三角形的外角性质等知识点的理解和掌握,此题关键是根据外角性质得∠2=∠1+∠C=∠1+∠B,这是此题的突破点.

练习册系列答案
相关题目
20.五个有理数的积为负数,则五个数中负数的个数是( )
| A. | 5或3 | B. | 3 | C. | 1 | D. | 1或3或5 |
19.有理数中,绝对值等于它本身的数是( )
| A. | 0 | B. | 0和1 | C. | 只有正数 | D. | 0和正数 |
20.下列说法中正确的选项是( )
| A. | 温度由-3℃上升3℃后达到-6℃ | |
| B. | 零减去一个数得这个数的相反数 | |
| C. | $\frac{π}{3}$既是分数,又是有理数 | |
| D. | 20.12既不是整数,也不是分数,所以它不是有理数 |
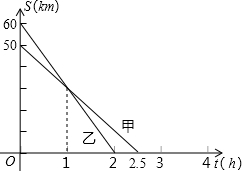 已知A、B、C三地在同一条笔直的公路上,甲、乙两人骑自行车分别从B、C两地前往A地.他们距A地的路程S(km)与行驶时间t(h)之间的关系如图所示,请根据图象所提供的信息解答下列问题:
已知A、B、C三地在同一条笔直的公路上,甲、乙两人骑自行车分别从B、C两地前往A地.他们距A地的路程S(km)与行驶时间t(h)之间的关系如图所示,请根据图象所提供的信息解答下列问题: 如图,已知数轴上点A表示的数为6,B是你数轴上一点,且AB=10,动点P从点O出发,以每秒6个单位长度的速度沿数轴向右匀速运动,设运动时间为t(t>0)秒.
如图,已知数轴上点A表示的数为6,B是你数轴上一点,且AB=10,动点P从点O出发,以每秒6个单位长度的速度沿数轴向右匀速运动,设运动时间为t(t>0)秒.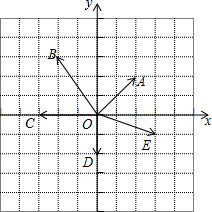 如图,在单位正方形网格中,建立直角坐标系,设$\overrightarrow{i}$、$\overrightarrow{j}$分别是x轴、y轴上的单位向量,试用$\overrightarrow{i}$、$\overrightarrow{j}$的线性组合表示下列在图中标出的向量.(直接将结果填在横线上)
如图,在单位正方形网格中,建立直角坐标系,设$\overrightarrow{i}$、$\overrightarrow{j}$分别是x轴、y轴上的单位向量,试用$\overrightarrow{i}$、$\overrightarrow{j}$的线性组合表示下列在图中标出的向量.(直接将结果填在横线上)  已知一块长方形绿地,在它的中央布置一个长方形花坛,四周铺上草地.设计的条件是这样的:绿地的长要比宽大4米,花坛四周的草地的宽都是2米,草地的总面积是80m2.求划出的这块长方形绿地的长和宽应当各是多少米?
已知一块长方形绿地,在它的中央布置一个长方形花坛,四周铺上草地.设计的条件是这样的:绿地的长要比宽大4米,花坛四周的草地的宽都是2米,草地的总面积是80m2.求划出的这块长方形绿地的长和宽应当各是多少米?