题目内容
1.计算:(1)3$\sqrt{5}$×2$\sqrt{10}$
(2)$\frac{\sqrt{20}+\sqrt{5}}{\sqrt{5}}$-2
(3)($\sqrt{5}$-$\frac{2}{\sqrt{5}}$)2
(4)3$\sqrt{20}$-$\sqrt{45}$-$\sqrt{\frac{1}{5}}$.
分析 (1)利用二次根式的乘法法则运算;
(2)先把$\sqrt{20}$化简,然后合并后进行二次根式的除法运算;
(3)利用平方差公式计算;
(4)先把各二次根式化为最简二次根式,然后合并即可.
解答 解:(1)原式=6$\sqrt{6×10}$
=12$\sqrt{15}$;
(2)原式=$\frac{2\sqrt{5}+\sqrt{5}}{\sqrt{5}}$-2
=$\frac{3\sqrt{5}}{\sqrt{5}}$-2
=3-2
=1;
(3)原式=5-4+$\frac{4}{5}$
=$\frac{9}{5}$;
(4)原式=6$\sqrt{5}$-3$\sqrt{5}$-$\frac{\sqrt{5}}{5}$
=$\frac{14\sqrt{5}}{5}$.
点评 本题考查了二次根式的计算:先把各二次根式化为最简二次根式,再进行二次根式的乘除运算,然后合并同类二次根式.在二次根式的混合运算中,如能结合题目特点,灵活运用二次根式的性质,选择恰当的解题途径,往往能事半功倍.

练习册系列答案
 作业辅导系列答案
作业辅导系列答案 同步学典一课多练系列答案
同步学典一课多练系列答案
相关题目
16.“双十一”期间,小王去水果批发市场采购苹果,他看中了A、B两家苹果.这两家苹果品质一样,零售价都为6元/千克,批发价各不相同.
A家规定:批发数量不超过1000千克,按零售价的92%优惠;批发数量不超过2000千克,按零售价的90%优惠;超过2000千克的按零售价的88%优惠.
B家的批发价格采用分段计算方法,规定如下表:
B家示例:小王批发苹果2100千克,总费用为(6×95%×500+6×85%×1000+6×75%×600)元.
(1)如果他批发800千克苹果,则他在A 家批发需要4416元,在B家批发需要4380元;
(2)如果他批发x千克苹果(1500<x≤2000),则他在A家批发需要$\frac{27}{5}$x元,在B家批发需要($\frac{9}{2}$x+1200)元(用含x的代数式表示);
(3)现在他要批发2000千克苹果,你能帮助他选择在哪家批发更优惠吗?请说明理由.
A家规定:批发数量不超过1000千克,按零售价的92%优惠;批发数量不超过2000千克,按零售价的90%优惠;超过2000千克的按零售价的88%优惠.
B家的批发价格采用分段计算方法,规定如下表:
| 数量范围 (千克) | 不超过500 | 超过500但不超过1500部分 | 超过1500但不超过2500部分 | 超过2500部分 |
| 价格 (元) | 零售价的95% | 零售价的85% | 零售价的75% | 零售价的70% |
(1)如果他批发800千克苹果,则他在A 家批发需要4416元,在B家批发需要4380元;
(2)如果他批发x千克苹果(1500<x≤2000),则他在A家批发需要$\frac{27}{5}$x元,在B家批发需要($\frac{9}{2}$x+1200)元(用含x的代数式表示);
(3)现在他要批发2000千克苹果,你能帮助他选择在哪家批发更优惠吗?请说明理由.
11.下列变形中属于因式分解的是( )
| A. | x2-2=(x+1)(x-1)-1 | B. | (x+2)(x-2)=x2-4 | C. | x2-2x+1=x(x-2)+1 | D. | x2-4=(x-2)(x+2) |
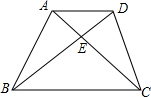 梯形ABCD中,AD∥BC,AC、BD交于E点,S△ADE:S△ADC=1:3,则S△ADE:S△DBC=$\frac{1}{4}$.
梯形ABCD中,AD∥BC,AC、BD交于E点,S△ADE:S△ADC=1:3,则S△ADE:S△DBC=$\frac{1}{4}$.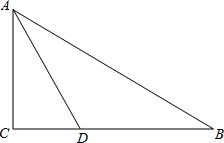 已知,如图,在Rt△ABC中,∠C=90°,∠BAC的角平分线AD交BC边于D.
已知,如图,在Rt△ABC中,∠C=90°,∠BAC的角平分线AD交BC边于D.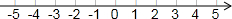 在数轴上把下列各数表示出来,并用“<”连接各数.
在数轴上把下列各数表示出来,并用“<”连接各数.