题目内容
4.某公司经过市场调查发现,该公司生产的某商品在第x天的售价(1≤x≤100)为(x+40)元/件,而该商品每天的销量满足关系式y=200-2x.如果该商品第20天的售价按7折出售,仍然可以获得40%的高额利润.(1)求该公司生产每件商品的成本为多少元;
(2)问销售该商品第几天时,每天的利润最大?最大利润是多少?
(3)该公司每天需要控制人工、水电和房租支出共计a元,若考虑这一因素后公司对最大利润要控制在4000元至5000元之间(包含4000和5000),且保证至少有90天的盈利,请直接写出a的取值范围.
分析 (1)设该公司生产每件商品的成本为a元,根据:实际售价-成本=利润,列出方程,解方程可得;
(2)根据:每天利润=单件利润×每天销售量列出函数关系式,配方成顶点式可得函数的最值情况;
(3)根据(2)中每天利润减去每天开支a元列出函数关系式P=-2(x-45)2+6050-a,根据最大利润要控制在4000元至5000元之间可得关于a的不等式,解不等式可得a的取值范围,再由至少有90天的盈利可知-2x2+180x+2000-a=0的两根x1、x2间距离x1-x2≥90,根据韦达定理可得关于a的不等式,求得a的范围,综合上述情况确定a的范围.
解答 解:(1)设该公司生产每件商品的成本为a元,根据题意,
得:0.7×(20+40)-a=0.4a,
解得:a=30,
故该公司生产每件商品的成本为30元;
(2)设第x天的销售利润为W,
则:W=(x+40-30)(-2x+200)=-2x2+180x+2000=-2(x-45)2+6050,
∴当x=45时,W取得最大值,最大值为6050元,
故问销售该商品第45天时,每天的利润最大,最大利润是6050元;
(3)记公司每天控制人工、水电和房租支出共计a元后利润为P,
则P=-2(x-45)2+6050-a,
根据题意:4000≤6050-a≤5000,
解得:1050≤a≤2050,
又∵至少有90天的盈利,
∴-2x2+180x+2000-a=0的两根x1、x2间距离x1-x2≥90,
∴(x1-x2)2≥902,即(x1+x2)2-4x1x2≥902,
∵x1+x2=90,x1x2=$\frac{a-2000}{2}$,
∴902-4×$\frac{a-2000}{2}$≥902,解得:a≤2000,
综上,1050≤a≤2000.
点评 本题主要考查二次函数的实际应用能力,明确不等关系并据此列出方程或函数关系式是解题基础,根据题意挖掘出不等关系求a的范围是关键.

| A. | m=-1且n=1 | B. | m=-1且n≠1 | C. | m=n=0 | D. | m≠1且n=1 |
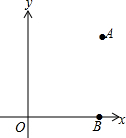 如图,在平面直角坐标系xOy中点A(6,8),点B(6,0).
如图,在平面直角坐标系xOy中点A(6,8),点B(6,0).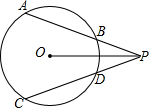 如图,已知过P点的两条直线交⊙O于A,B,C,D四点,且OP平分∠APC.
如图,已知过P点的两条直线交⊙O于A,B,C,D四点,且OP平分∠APC. 有理数a、b、c在数轴上的位置如图所示,化简:|c|-|b+c|+|c-a|+|b+a|.
有理数a、b、c在数轴上的位置如图所示,化简:|c|-|b+c|+|c-a|+|b+a|.