题目内容
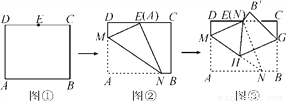
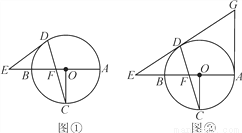
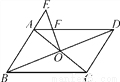
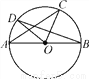
如图,在矩形ABCD中,AB=8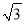 ,AD=10,点E是CD的中点,将这张纸片依次折叠两次:第一次折叠纸片使点A与点E重合,如图②,折痕为MN,连接ME,NE;第二次折叠纸片使点N与点E重合,如图③,点B落到B′处,折痕为HG,连接HE,则下列结论:①ME∥HG;②△MEH是等边三角形;③∠EHG=∠AMN;④tan∠EHG=
,AD=10,点E是CD的中点,将这张纸片依次折叠两次:第一次折叠纸片使点A与点E重合,如图②,折痕为MN,连接ME,NE;第二次折叠纸片使点N与点E重合,如图③,点B落到B′处,折痕为HG,连接HE,则下列结论:①ME∥HG;②△MEH是等边三角形;③∠EHG=∠AMN;④tan∠EHG=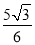 .其中正确的个数是( )
.其中正确的个数是( )
A. 1个 B. 2个 C. 3个 D. 4个
C 【解析】【解析】 如图③,由折叠可得,∠MEN=∠A=90°,HG⊥NE,即ME⊥EN,HG⊥EN,∴EM∥GH,故①正确; ∵EM∥GH,∴∠NME=∠NHG,由折叠可得,∠NME=∠AMN,∠EHG=∠NHG,∴∠AMN=∠EHG,故③正确; 如图2,作NF⊥CD于F.设DM=x,则AM=EM=10﹣x.∵点E是CD的中点,AB=CD=,∴DE=CD=.在Rt△DEM中...
练习册系列答案
相关题目


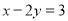 ,那么代数式
,那么代数式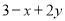 的值是( )
的值是( )
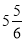 +(﹣9
+(﹣9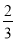 )+17
)+17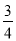 +(﹣3
+(﹣3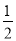 )
)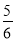 )]+[(﹣9)+(﹣
)]+[(﹣9)+(﹣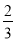 )]+[(+17)+(+
)]+[(+17)+(+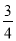 )]+[(﹣3)+(﹣
)]+[(﹣3)+(﹣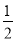 )]
)]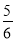 )+(﹣
)+(﹣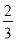 )+(+
)+(+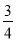 )+(﹣
)+(﹣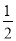 )]
)]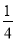 )
)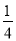
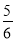 )+(﹣2007
)+(﹣2007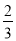 )+4017
)+4017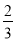 +(﹣1
+(﹣1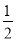 )
)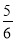 )+(-
)+(-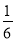 )=
)= 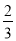 ;⑤- (-
;⑤- (-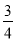 ) + (-7
) + (-7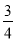 ) = 7.
) = 7.