Question

3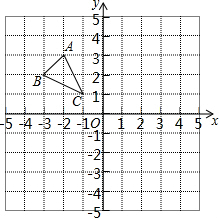．如图，已知△ABC的三个顶点在格点上．
（1）作出与△ABC关于x轴对称的图形△A₁B₁C₁；
（2）则△A₁B₁C₁的面积是1.5；
（3）若点P在△ABC内的坐标是（a，b），则点P在△A₁B₁C₁中对应点P′的坐标是（a，-b）．

Answer 1

分析 （1）首先确定A、B、C关于x轴的对称点的位置，再连接即可；
（2）利用矩形面积减去周围多余三角形的面积可得答案；
（3）根据关于x轴对称点的坐标特点：横坐标不变，纵坐标相反可得答案．

解答 解：（1）如图所示：

（2）△A₁B₁C₁的面积是：2×2-$\frac{1}{2}$×2×1-$\frac{1}{2}×$1×1-$\frac{1}{2}$×1×2=1.5，
故答案为：1.5；

（3）∵△ABC和△A₁B₁C₁关于x轴对称，
∴△ABC上所有点与△A₁B₁C₁上的对应点横坐标不变，纵坐标相反，
∵点P在△ABC内的坐标是（a，b），
∴点P在△A₁B₁C₁中对应点P′的坐标是（a，-b），
故答案为：（a，-b）．

点评 此题主要考查了作图--轴对称变换，以及关于x轴对称点的坐标特点，几何图形都可看做是有点组成，画一个图形的轴对称图形时，也就是确定一些特殊点的对称点．