题目内容
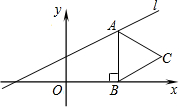 如图,点A在直线l:y=
如图,点A在直线l:y=| 1 |
| 2 |
(1)求点C的坐标;
(2)将△ABC向左平移,当点C的对应点C′落在直线l上时,求平移的距离.
考点:一次函数图象上点的坐标特征,等边三角形的性质,坐标与图形变化-平移
专题:
分析:(1)先把y=2代入直线y=
x+1求出x的值,再过C作CD⊥AB于点D,根据等边三角形的性质求出BD的长,再根据勾股定理求出CD的长,进而得出C点坐标;
(2)把y=1代入y=
x+1求出x的值,故可得出C′的坐标,求出CC′的长即可得出结论.
| 1 |
| 2 |
(2)把y=1代入y=
| 1 |
| 2 |
解答: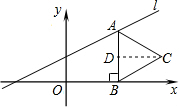 解:(1)∵AB⊥x轴,且AB=2.
解:(1)∵AB⊥x轴,且AB=2.
∴把y=2代入y=
x+1,得x=2,即OB=2.
过C作CD⊥AB于点D,则BD=
AB=1,BC=2,
∴CD=
=
.
∴C(2+
,1);
(2)当点C的对应点C′落在直线l上时,
∵把y=1代入y=
x+1得x=0,
∴C′(0,1).
∴CC′=2+
,即平移的距离为2+
.
 解:(1)∵AB⊥x轴,且AB=2.
解:(1)∵AB⊥x轴,且AB=2.∴把y=2代入y=
| 1 |
| 2 |
过C作CD⊥AB于点D,则BD=
| 1 |
| 2 |
∴CD=
| BC2-BD2 |
| 3 |
∴C(2+
| 3 |
(2)当点C的对应点C′落在直线l上时,
∵把y=1代入y=
| 1 |
| 2 |
∴C′(0,1).
∴CC′=2+
| 3 |
| 3 |
点评:本题考查的是一次函数图象上点的坐标特点,熟知一次函数图象上各点的坐标一定适合此函数的解析式是解答此题的关键.

练习册系列答案
相关题目
下列数据中,哪一组数能作为直角三角形的三边长( )
| A、9,12,15 |
| B、3,4,6 |
| C、1,2,3 |
| D、6,9,11 |
 如图,面积为48cm2的正方形纸板四个角是面积为3cm2的小正方形,现将四个小正方形剪掉,制作一个无盖的长方体盒子.
如图,面积为48cm2的正方形纸板四个角是面积为3cm2的小正方形,现将四个小正方形剪掉,制作一个无盖的长方体盒子.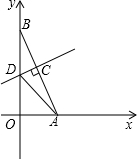 已知如图,在平面直角坐标系中,点A、B分别在x轴、y轴上,线段OA、OB的长(OA<OB)是方程x2-18x+72=0的两个根,且AC:BC=3:2,过点C作AB的垂线交y轴于点D.
已知如图,在平面直角坐标系中,点A、B分别在x轴、y轴上,线段OA、OB的长(OA<OB)是方程x2-18x+72=0的两个根,且AC:BC=3:2,过点C作AB的垂线交y轴于点D. (1)解不等式
(1)解不等式