题目内容
 如图,BD、CE分别是△ABC的两边上的高,过D作DG⊥BC于G,分别交CE及BA的延长线于F、H,求证:
如图,BD、CE分别是△ABC的两边上的高,过D作DG⊥BC于G,分别交CE及BA的延长线于F、H,求证:(1)DG2=BG•CG;
(2)BG•CG=GF•GH.
考点:相似三角形的判定与性质
专题:证明题
分析:(1)根据题意结合图形,证明△BDC∽△DGC,列出比例式,化为等积式即可解决问题.
(2)方法同(1)中的解法,证明△BGH∽△FGC,列出比例式,化为等积式即可解决问题.
(2)方法同(1)中的解法,证明△BGH∽△FGC,列出比例式,化为等积式即可解决问题.
解答: 证明:(1)∵BD⊥AC,DG⊥BC,
证明:(1)∵BD⊥AC,DG⊥BC,
∴∠BDC=∠DGC=90°,
∠DBC+∠DCG=∠GDC+∠DCG,
∴∠GDC=∠DBC,
∴△BDC∽△DGC,
∴BG:DG=DG:CG,
即DG2=BG•CG.
(2)同(1)中的方法,同理可证:△BGH∽△FGC,
∴BG:GF=GH:CG,
∴BG•CG=GF•GH.
 证明:(1)∵BD⊥AC,DG⊥BC,
证明:(1)∵BD⊥AC,DG⊥BC,∴∠BDC=∠DGC=90°,
∠DBC+∠DCG=∠GDC+∠DCG,
∴∠GDC=∠DBC,
∴△BDC∽△DGC,
∴BG:DG=DG:CG,
即DG2=BG•CG.
(2)同(1)中的方法,同理可证:△BGH∽△FGC,
∴BG:GF=GH:CG,
∴BG•CG=GF•GH.
点评:该题主要考查了相似三角形的判定及其性质的应用问题;解题的关键是深入观察分析、大胆猜测推理、合情变式探究、科学解答论证.

练习册系列答案
相关题目
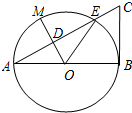 如图,以线段AB为直径的⊙O交线段AC于点E,点D是AE的中点,连接OD并延长交⊙O于点M,∠BOE=60°,cosC=
如图,以线段AB为直径的⊙O交线段AC于点E,点D是AE的中点,连接OD并延长交⊙O于点M,∠BOE=60°,cosC= 如图,在平面直角坐标系中,矩形OABC的对角线AC所在的直线的解析式为y=-
如图,在平面直角坐标系中,矩形OABC的对角线AC所在的直线的解析式为y=- 如图,在Rt△ABC中,AB=AC,点D为BC的中点,∠MDN=90°,∠MDN绕点D旋转,DM、DN分别与边AB、AC交于E、F两点,若AB=4cm,求线段EF长度的最小值.
如图,在Rt△ABC中,AB=AC,点D为BC的中点,∠MDN=90°,∠MDN绕点D旋转,DM、DN分别与边AB、AC交于E、F两点,若AB=4cm,求线段EF长度的最小值.