题目内容
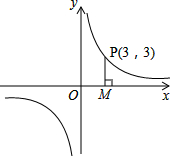 已知反比例函数(k为常数,k≠0)的图象经过P(3,3),O为坐标原点,
已知反比例函数(k为常数,k≠0)的图象经过P(3,3),O为坐标原点,(1)求k的值;
(2)过点P作PM⊥x轴于M,若点Q在反比例函数第一象限的图象上,并且△QOM的面积为6,试求Q点的坐标.
考点:反比例函数图象上点的坐标特征,反比例函数系数k的几何意义
专题:
分析:(1)直接把点(3,3)代入反比例函数y=
(k≠0),求出k的值即可;
(2)设Q点的纵坐标为y,再根据△QOM的面积为6求出y的值,进而可得出Q点的坐标.
| k |
| x |
(2)设Q点的纵坐标为y,再根据△QOM的面积为6求出y的值,进而可得出Q点的坐标.
解答:解:(1)∵反比例函数y=
(k为常数,k≠0)的图象经过P(3,3),
∴3=
,
解得k=9;
(2)设Q点的纵坐标为y,
则S△QOM=
×3y=6,
解得y=4,
∵将y=4,k=9代入反比例函数y=
得,x=
,
∴Q(
,4).
| k |
| x |
∴3=
| k |
| 3 |
解得k=9;
(2)设Q点的纵坐标为y,
则S△QOM=
| 1 |
| 2 |
解得y=4,
∵将y=4,k=9代入反比例函数y=
| k |
| x |
| 9 |
| 4 |
∴Q(
| 9 |
| 4 |
点评:本题考查的是反比例函数图象上点的坐标特点,熟知反比例函数图象上各点的坐标一定适合此函数的解析式是解答此题的关键.

练习册系列答案
 黄冈小状元满分冲刺微测验系列答案
黄冈小状元满分冲刺微测验系列答案 新辅教导学系列答案
新辅教导学系列答案 阳光同学一线名师全优好卷系列答案
阳光同学一线名师全优好卷系列答案
相关题目
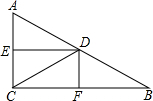 已知,如图,在△ABC中,∠ACB=90°,D是AB的中点,DE、DF分别是△BDC、△ADC的角平分线.求证:四边形DECF是矩形.
已知,如图,在△ABC中,∠ACB=90°,D是AB的中点,DE、DF分别是△BDC、△ADC的角平分线.求证:四边形DECF是矩形. 如图,AC=3,BC=4,AD=13,求△ABD的面积.
如图,AC=3,BC=4,AD=13,求△ABD的面积.