题目内容
已知二次函数y = ax2的图象经过点(2,1).
(1)求二次函数y = ax2的解析式;
(2)一次函数y = mx+4的图象与二次函数y = ax2的图象交于A(x1、y1)、B(x2、y2)两点.
①当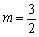 时(图①),求证:△AOB为直角三角形;
时(图①),求证:△AOB为直角三角形;
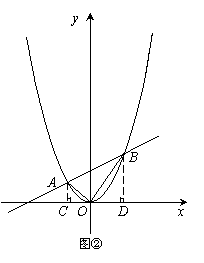
②试判断当 时(图②),△AOB的形状,并证明;
时(图②),△AOB的形状,并证明;
(3)根据第(2)问,说出一条你能得到的结论.(不要求证明)
 |
解:(1)由条件得1 = 4a,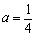 ,所以二次函数的解析式是
,所以二次函数的解析式是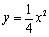 …………………1分
…………………1分
 (2)①由
(2)①由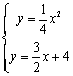 得
得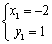 ,
,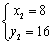 ,
,
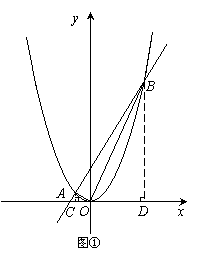
即A(-2,1),B(8,16)…………………………3分
过A作AC⊥x轴于C,过B作BD⊥x轴于D,
则AC = 1,OC = 2,OD = 8,BD = 16,
∴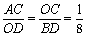 又∵∠ACO =∠ODB = 90º
又∵∠ACO =∠ODB = 90º
∴△ACO ∽ △ODB ………………………………4分
∴∠AOC = ∠OBD
∴∠AOC +∠BOD = 90º
∴∠AOB = 90º
∴△AO B为直角三角形 …………………………………………………………
B为直角三角形 …………………………………………………………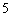 分
分
②△AOB为直角三角形, ………………………………………………………………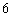 分
分
 证明如下:
证明如下:
过A作AC⊥x轴于C,过B作BD⊥x轴于D
由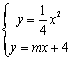 得x2-4mx-16 = 0
得x2-4mx-16 = 0
解得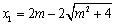 ,
, …………
…………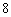 分
分
∴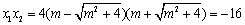
∴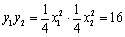 …………
………… …………………
…………………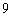 分
分
∴OC•OD = AC•BD = 16
∴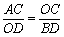 …………………………………………
………………………………………… ……………………………
…………………………… 分
分
又∵∠ACO =∠ODB = 90º,∴△ACO ∽△ODB ……………………………… 分
分
∴∠AOC =∠OBD
∴∠AOC +∠BOD =90º ∴∠AOB =90º
∴△AOB为直角三角形.
(3)可能的结论为 …………………………………………………………………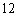 分
分
如果过定点(0,4)的直线与抛物线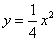 交于A、B两点,O为抛物线的顶点,那么△AOB必为直角三角形.
交于A、B两点,O为抛物线的顶点,那么△AOB必为直角三角形.
如果过定点(0, )的直线与抛物线
)的直线与抛物线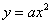 交于A、B两点,O为抛物线的顶点,那么△AOB必为直角三角形.
交于A、B两点,O为抛物线的顶点,那么△AOB必为直角三角形.

 的解集为 .
的解集为 .
 的图像与
的图像与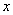 轴、
轴、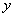 轴分别相交于点A、B,点P在该函数图像上, P到
轴分别相交于点A、B,点P在该函数图像上, P到 、
、 。
。 的值;
的值; 时点P的坐标;
时点P的坐标;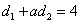 (
(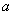 为常数), 求
为常数), 求

 ,且
,且 ,那么k = .
,那么k = . .
. 如图,
如图, =30°,
=30°, 为
为 上一点,且
上一点,且 =6,以点
=6,以点 的圆与
的圆与 的位置关系是( )
的位置关系是( ) .
.