题目内容
8. 如图所示,平行四边形ABCD中,顶点A、B、D在坐标轴上,AD=5,AB=9,点A的坐标为(-3,0),则点C的坐标为(9,4).
如图所示,平行四边形ABCD中,顶点A、B、D在坐标轴上,AD=5,AB=9,点A的坐标为(-3,0),则点C的坐标为(9,4).
分析 由平行四边形的性质得出CD=AB=9,由勾股定理求出OD,即可得出点C的坐标.
解答 解:∵四边形ABCD是平行四边形,
∴CD=AB=9,
∵点A的坐标为(-3,0),
∴OA=3,
∴OD=$\sqrt{A{D}^{2}-O{A}^{2}}$=$\sqrt{{5}^{2}-{3}^{2}}$=4,
∴点C的坐标为(9,4).
故答案为:(9,4).
点评 本题考查了平行四边形的性质、坐标与图形性质、勾股定理;熟练掌握平行四边形的性质,由勾股定理求出OD是解决问题的关键.

练习册系列答案
 超能学典单元期中期末专题冲刺100分系列答案
超能学典单元期中期末专题冲刺100分系列答案 黄冈360度定制密卷系列答案
黄冈360度定制密卷系列答案 阳光考场单元测试卷系列答案
阳光考场单元测试卷系列答案 名校联盟冲刺卷系列答案
名校联盟冲刺卷系列答案
相关题目
16.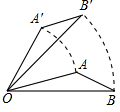 如图,将△AOB绕点O按逆时针方向旋转60°后得到△A′OB′,若∠AOB=15°,则∠AOB′的度数是( )
如图,将△AOB绕点O按逆时针方向旋转60°后得到△A′OB′,若∠AOB=15°,则∠AOB′的度数是( )
 如图,将△AOB绕点O按逆时针方向旋转60°后得到△A′OB′,若∠AOB=15°,则∠AOB′的度数是( )
如图,将△AOB绕点O按逆时针方向旋转60°后得到△A′OB′,若∠AOB=15°,则∠AOB′的度数是( )| A. | 40° | B. | 45° | C. | 50° | D. | 55° |
13.下列数据不能确定物体位置的是( )
| A. | 2楼4号 | B. | 大学路19号 | C. | 北偏东60° | D. | 东经111°北纬40° |
17.在平面直角坐标系中,将点(-2,3)关于原点的对称点向右平移2个单位长度得到的点的坐标是( )
| A. | (4,-3) | B. | (-4,3) | C. | (0,-3) | D. | (0,3) |
 如图,点M在∠AOB的边OB上.
如图,点M在∠AOB的边OB上. 已知:抛物线y=x2+2mx+m,m为常数.
已知:抛物线y=x2+2mx+m,m为常数. 如图,将BM′绕点O按逆时针方向旋转45°后得到△A′OB′,若△AOB=15°,则∠AOB′的度数是30°.
如图,将BM′绕点O按逆时针方向旋转45°后得到△A′OB′,若△AOB=15°,则∠AOB′的度数是30°.
 如图,将△ABC绕点B顺时针旋转40°得到△DBE,若此时点A的对应点D恰好落在边AC上,且∠ABE=90°,则∠C的度数为60°.
如图,将△ABC绕点B顺时针旋转40°得到△DBE,若此时点A的对应点D恰好落在边AC上,且∠ABE=90°,则∠C的度数为60°.