题目内容
已知,二次函数y=x2-(m-1)x+m的图象交x轴于A(x1,0),B(x2,0)两点,交y轴的正半轴于点C,且x12+x22=10.(已知存在如下关系:x1x2=m,x1+x2=m-1),求二次函数的解析式.
考点:抛物线与x轴的交点
专题:
分析:本题是用待定系数法求二次函数的解析式,由图象与x轴交于点A(x1,0)、B(x2,0)两点,就相当于方程x2-(m-1)x+m=0两个根分别为x1,x2,由两根关系求解代入二次函数即可.
解答:解:∵二次函数y=x2-(m-1)x+m的图象交x轴于A(x1,0),B(x2,0)两点,
∴x1x2=m,x1+x2=m-1.
∴x12+x22=(x1+x2)2-2x1x2=(m-1)2-2m=10,
解得 m1=2+
,m2=2-
.
则-(m-1)=
-1或-(m-1)=
-3.
故抛物线的解析式为:y=x2-(
-1)x+2+
或y=x2-(
-3)x+2-
.
∴x1x2=m,x1+x2=m-1.
∴x12+x22=(x1+x2)2-2x1x2=(m-1)2-2m=10,
解得 m1=2+
| 13 |
| 13 |
则-(m-1)=
| 13 |
| 13 |
故抛物线的解析式为:y=x2-(
| 13 |
| 13 |
| 13 |
| 13 |
点评:本题考查了抛物线与x轴的交点.注意使用一元二次方程根与系数的关系求解关于两根的问题.

练习册系列答案
 寒假大串联黄山书社系列答案
寒假大串联黄山书社系列答案 寒假创新型自主学习第三学期寒假衔接系列答案
寒假创新型自主学习第三学期寒假衔接系列答案
相关题目
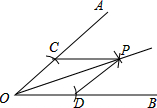 用尺规作图作∠AOB的平分线的方法如下:以O为圆心,任意长为半径画弧交OA,OB于点C,D,再分别以点C,D为圆心,以大于
用尺规作图作∠AOB的平分线的方法如下:以O为圆心,任意长为半径画弧交OA,OB于点C,D,再分别以点C,D为圆心,以大于 已知:如图,在四边形ABCD中,AB∥CD,AE⊥BD,CF⊥BD,垂足分别为E、F,且AE=CF,求证:AB=CD.
已知:如图,在四边形ABCD中,AB∥CD,AE⊥BD,CF⊥BD,垂足分别为E、F,且AE=CF,求证:AB=CD. 已知,如图,点B、C在线段AD上,AB=CD,EA⊥AD,BF⊥BD,CE=DF,求证:CE∥DF.
已知,如图,点B、C在线段AD上,AB=CD,EA⊥AD,BF⊥BD,CE=DF,求证:CE∥DF. 如图,某小区广场要修建一个矩形花坛,花坛的长、宽分别为100m和60m,花坛中有一横、两纵的通道,横、纵通道的宽度分别为2xcm和xcm.
如图,某小区广场要修建一个矩形花坛,花坛的长、宽分别为100m和60m,花坛中有一横、两纵的通道,横、纵通道的宽度分别为2xcm和xcm. 抛物线y=ax2+ax+c(a≠0)与x轴交于A、B两点(A在B的左边),与y轴交于点C,AB=3,且抛物线过点P(-1,3),求抛物线的解析式.
抛物线y=ax2+ax+c(a≠0)与x轴交于A、B两点(A在B的左边),与y轴交于点C,AB=3,且抛物线过点P(-1,3),求抛物线的解析式.