题目内容
如图14.1,在梯形ABCD中,AD//BC,点M、N分别在边AB、DC上![]() ,且MN//AD,记AD=a ,BC=b.
,且MN//AD,记AD=a ,BC=b.
若 ![]() =
= ![]() ,则有结论:MN =
,则有结论:MN = ![]() .请根据以上结论,解答下列问题:
.请根据以上结论,解答下列问题:
如图14.2、14.3,BE、CF是△ABC的两条角平分线,过EF上一点P分别作△ABC三边的垂线段PP1、PP2、PP3,交BC于点P1,交AB于点P2, 交AC于点P3 .
交AC于点P3 .
(1)若点P为线段EF的中点,求证: PP1 = PP2 + PP3 ;
(2)若点P为线段EF上的任意点,试探究PP1、PP2、PP3的数量关系,并给出证明。

解:(1)证明:过点E分别作BC、AB的垂线,垂足分别为M、N,过点F分别作BC、AC的垂线,垂足分别为G、H。
BE、CF分别为∠ABC、∠ACB的角平分线,EN=EM,FH=FG,
PP2//EN,PP3//FH,点P为线段EF的中点,PP2=![]() EN=
EN=![]() EM,PP3=
EM,PP3=![]() FH=
FH=![]() FG.
FG.
PP1//FG//EM , ![]() , PP1=
, PP1= ![]() =
= ![]() =
=![]() FG+
FG+ ![]() EM = PP2+ PP3.
EM = PP2+ PP3.
(2) PP1= PP2+ PP3.
证明:过点E分别作BC、AB的垂线,垂足分别为M、N,过点F分别作BC、AC的垂线,垂足分别为G、H。
令FG = a ,EM = b, ![]() =
= ![]() , PP1//FG//EM , PP1=
, PP1//FG//EM , PP1= ![]() ;
;
EM=EN, ![]() =
= ![]() =
= ![]() ,PP2=
,PP2= ![]() ·EN=
·EN= ![]() ·EM=
·EM= ![]() ;
;
同理可得:PP3 = ![]() ·FH =
·FH = ![]() ·FG =
·FG = ![]() ;
;![]() +
+ ![]() =
= ![]() ,
,
PP1= PP2+ PP3.

练习册系列答案
 阅读快车系列答案
阅读快车系列答案
相关题目
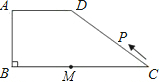 如图所示,在梯形ABCD中,AD∥BC,∠ABC=90°,AD=AB=6,BC=14,点M是线段BC上一定点,且MC=8.动点P从C点出发沿C?D?A?B的路线运动,运动到点B停止.在点P的运动过程中,使△PMC为等腰三角形的点P有
如图所示,在梯形ABCD中,AD∥BC,∠ABC=90°,AD=AB=6,BC=14,点M是线段BC上一定点,且MC=8.动点P从C点出发沿C?D?A?B的路线运动,运动到点B停止.在点P的运动过程中,使△PMC为等腰三角形的点P有 如图所示.在梯形ABCD中,AB∥CD.若△DCE的面积是△DCB的面积的
如图所示.在梯形ABCD中,AB∥CD.若△DCE的面积是△DCB的面积的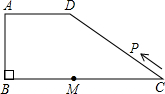 如图所示,在梯形ABCD中,AD∥BC,∠ABC=90°,AD=AB=6,BC=14,点M是线段BC上一定点,且MC=8.动点P从C点出发沿C→D→A→B的路线运动,运动到点B停止.在点P的运动过程中,使△PMC为等腰三角形的点P有几个?并求出相应等腰三角形的腰长.
如图所示,在梯形ABCD中,AD∥BC,∠ABC=90°,AD=AB=6,BC=14,点M是线段BC上一定点,且MC=8.动点P从C点出发沿C→D→A→B的路线运动,运动到点B停止.在点P的运动过程中,使△PMC为等腰三角形的点P有几个?并求出相应等腰三角形的腰长.