题目内容
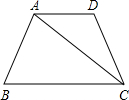
 如图所示.在梯形ABCD中,AB∥CD.若△DCE的面积是△DCB的面积的
如图所示.在梯形ABCD中,AB∥CD.若△DCE的面积是△DCB的面积的| 1 | 4 |
分析:因为AB∥CD,所以△DCE∽△BEA,又△DCE和△CBE等高,△DCE的面积是△DCB的面积的
,∴
=3,所以△ABE的面积是△DCE面积的9倍,△AED和△BEC的面积相等,△ABD的面积等于△AEB的面积加上△AED的面积,所以△DCE的面积是△ABD的面积十二分之一.
| 1 |
| 4 |
| BE |
| DE |
解答:解:∵△DCE的面积是△DCB的面积的
∴△DCE的面积是△BCE面积的
∵△DCE和△BCE等高
∴
=
因为AB∥CD,所以△DCE∽△BEA
∴
=
又∵△DEA和△ECB的面积相等
∴所以△DCE的面积是△ABD的面积十二分之一
| 1 |
| 4 |
∴△DCE的面积是△BCE面积的
| 1 |
| 3 |
∵△DCE和△BCE等高
∴
| DE |
| EB |
| 1 |
| 3 |
因为AB∥CD,所以△DCE∽△BEA
∴
| △DEC |
| △AEB |
| 1 |
| 9 |
又∵△DEA和△ECB的面积相等
∴所以△DCE的面积是△ABD的面积十二分之一
点评:本题考查相似三角形的判定和性质以及对求三角形面积时等底等高情况的灵活运用.

练习册系列答案
 阅读快车系列答案
阅读快车系列答案
相关题目
 已知如图所示,在梯形ABCD中,AD∥BC,AB=AD=DC=8,∠B=60°,连接AC.
已知如图所示,在梯形ABCD中,AD∥BC,AB=AD=DC=8,∠B=60°,连接AC. 如图所示,在梯形ABCD中,AD∥BC,∠ABC=90°,AD=AB=6,BC=14,点M是线段BC上一定点,且MC=8.动点P从C点出发沿C?D?A?B的路线运动,运动到点B停止.在点P的运动过程中,使△PMC为等腰三角形的点P有
如图所示,在梯形ABCD中,AD∥BC,∠ABC=90°,AD=AB=6,BC=14,点M是线段BC上一定点,且MC=8.动点P从C点出发沿C?D?A?B的路线运动,运动到点B停止.在点P的运动过程中,使△PMC为等腰三角形的点P有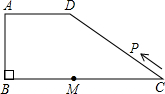 如图所示,在梯形ABCD中,AD∥BC,∠ABC=90°,AD=AB=6,BC=14,点M是线段BC上一定点,且MC=8.动点P从C点出发沿C→D→A→B的路线运动,运动到点B停止.在点P的运动过程中,使△PMC为等腰三角形的点P有几个?并求出相应等腰三角形的腰长.
如图所示,在梯形ABCD中,AD∥BC,∠ABC=90°,AD=AB=6,BC=14,点M是线段BC上一定点,且MC=8.动点P从C点出发沿C→D→A→B的路线运动,运动到点B停止.在点P的运动过程中,使△PMC为等腰三角形的点P有几个?并求出相应等腰三角形的腰长.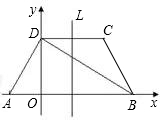 如图所示,在梯形ABCD中,已知AB∥CD,AD⊥DB,AD=DC=CB,AB=4,DO垂直于AB.则腰长是
如图所示,在梯形ABCD中,已知AB∥CD,AD⊥DB,AD=DC=CB,AB=4,DO垂直于AB.则腰长是 如图所示,在梯形ABCD中,AB∥DC,EF是梯形的中位线,AC交EF于G,BD交EF于H,以下说法错误的是( )
如图所示,在梯形ABCD中,AB∥DC,EF是梯形的中位线,AC交EF于G,BD交EF于H,以下说法错误的是( )