题目内容
3.生活中有些量只有大小没有方向,如长度、面积等;有些量既有大小又有方向,比如力、速度等,我们把既有大小又有方向的量叫向量,以A为起点,B为终点的向量用符号$\overrightarrow{AB}$表示,两个向量可以相加,其法则是平行四边形法则.如图1中,四边形ABCD是平行四边形,则向量$\overrightarrow{AB}$与向量$\overrightarrow{AD}$的和等于向量$\overrightarrow{AC}$,即$\overrightarrow{AB}$+$\overrightarrow{AD}$=$\overrightarrow{AC}$.利用上述法则解决下面的问题:
小明的爸爸是武汉“大桥冬泳队”队员,已知某一天长江的水速为2km/h(图2中的$\overrightarrow{AD}$),若小明的爸爸在静水中的速度为2$\sqrt{3}$km/h,那么从A点出发沿与沿岸垂直的方向游到对岸去(图2中的$\overrightarrow{AB}$),求小明的爸爸游到对岸的实际速度的大小和方向(图2中的$\overrightarrow{AC}$).
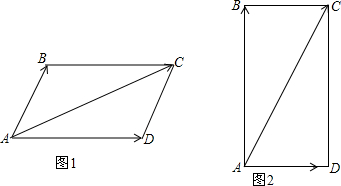
分析 此题实际上是求AC的长度和∠DAC的大小.通过解直角△ADC可以求得∠DAC的度数,根据$\overrightarrow{AB}$+$\overrightarrow{AD}$=$\overrightarrow{AC}$来求$\overrightarrow{AC}$.
解答 解:依题意得:AD=2,DC=AB=2$\sqrt{3}$,∠ADC=90°.
∵在直角△ADC中,tan∠∠DAC=$\frac{CD}{AD}$=$\frac{2\sqrt{3}}{2}$=$\sqrt{3}$,
∴∠DAC=60°,
又∵$\overrightarrow{AD}$=2,$\overrightarrow{AB}$=2$\sqrt{3}$,
∴|$\overrightarrow{AC}$|=|$\overrightarrow{AB}$+$\overrightarrow{AD}$|=$\sqrt{{2}^{2}+(2\sqrt{3})^{2}}$=4.
答:小明爸爸游到对岸的实际速度是4km/h,方向与河岸成60°夹角.
点评 本题考查了平面向量.理解平行四边形法则是解题的关键.

练习册系列答案
相关题目
17.若x1、x2是二次函数y=x2+4x+3与x轴交点的横坐标,那么x1x2的值是( )
| A. | 4 | B. | 3 | C. | -4 | D. | -3 |
 如图,已知正五边形ABCDE中,∠1=∠2,∠3=∠4,求角x的度数.
如图,已知正五边形ABCDE中,∠1=∠2,∠3=∠4,求角x的度数.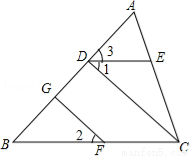
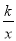 与y=﹣kx2+k(k≠0)在同一直角坐标系中的图象可能是( )
与y=﹣kx2+k(k≠0)在同一直角坐标系中的图象可能是( ) B.
B.  C.
C.  D.
D. 