题目内容
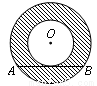
如图,边长为4cm的等边三角形ABC与⊙O等高(即高与直径相等),⊙O与BC相切于点C,⊙O与AC相交于点E.

求:(1)CE的长;
(2)阴影部分的面积.
【解析】
试题分析:(1)连接OC,并过点O作OF⊥CE于F,根据等边三角形的性质,等边三角形的高等于底边的 倍.已知边长为4cm的等边三角形ABC与⊙O等高,说明⊙O的半径为
倍.已知边长为4cm的等边三角形ABC与⊙O等高,说明⊙O的半径为 ,即OC=
,即OC= ,又∠ACB=60°,故有∠OCF=30°,在Rt△OFC中,可得出FC的长,利用垂径定理即可得出CE的长.
,又∠ACB=60°,故有∠OCF=30°,在Rt△OFC中,可得出FC的长,利用垂径定理即可得出CE的长.
(2)过点A作AE⊥BC于点E,过点O作OF⊥AC于点F,根据等腰三角形的性质求出AE的长,由三角形ABC与⊙O等高即可得出圆的半径,再根据⊙O与BC相切于点C可知OC⊥BC,故可得出∠OCD的度数,由三角形内角和定理求出∠COD的度数,根据直角三角形的性质求出OF及CF的长,由S阴影=S扇形-S△OCD即看得出结论.
试题解析:(1)连接OC,并过点O作OF⊥CE于F,

且△ABC为等边三角形,边长为4,
故高为2 ,即OC=
,即OC= ,
,
又∠ACB=60°,故有∠OCF=30°,
在Rt△OFC中,可得 ,FC=1.5,即CE=3.
,FC=1.5,即CE=3.
(2)S阴影=S扇形OCE-S△OCE=
考点:1.切线的性质;2.垂径定理;3.圆周角定理;4.扇形面积的计算

练习册系列答案
相关题目

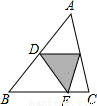
 (x>0)上,点D在双曲线y=-
(x>0)上,点D在双曲线y=-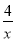 (x<0)上,点A和点C分别在x轴,y轴的正半轴上,且点A,B,C,D构成的四边形为正方形.求:
(x<0)上,点A和点C分别在x轴,y轴的正半轴上,且点A,B,C,D构成的四边形为正方形.求: