Question

【题目】如图，△ABC中，AD平分∠BAC，DE⊥AB于点E且AE=8cm，F为AE的中点，G从A点向C点以每秒1个单位的速度运动，则点G经过_______秒时DG=DF．

Answer 1

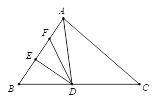
【答案】4或12

【解析】

根据角平分线的性质可得DE=DH，易证Rt△AED≌Rt△AHD，得到AE=AH=8cm，然后由DG=DF可得Rt△EFD≌Rt△HGD，可得HG=EF=4cm，同理可得HG’=4cm，易求答案.

解：作DH⊥AC，DG

∵AD平分∠BAC，DE⊥AB，DH⊥AC，

∴DE=DH，∠AED=∠AHD=90°，

∵AD=AD，

∴Rt△AED≌Rt△AHD（HL），

∴AE=AH=8cm，

在Rt△EFD和Rt△HGD中，DE=DH,

∴当DG=DF时，Rt△EFD≌Rt△HGD，

∴HG=EF，

∵F为AE的中点，

∴EF=4cm，

∴HG=4cm，

同理可得HG’=4cm，

∴AG=8-4=4cm，AG’=8+4=12cm，

∵G从A点向C点以每秒1个单位的速度运动，

∴点G经过4秒或12秒时DG=DF.