Question

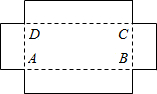如图，用一块长为50cm、宽为30cm的长方形铁片制作一个无盖的盒子，若在铁片的四个角截去四个相同的小正方形，设小正方形的边长为xcm．
（1）底面的长AB=

50-2x

cm，宽BC=

30-2x

cm（用含x的代数式表示）
（2）当做成盒子的底面积为300cm²时，求该盒子的容积．

Answer 1

分析：（1）利用长方形的长与宽以及在铁片的四个角截去四个相同的小正方形，得出AB与BC的长即可；
（2）利用（1）中长与宽以及盒子的底面积为300cm²时得出x的值，即可的求出盒子的容积；

解答：解：（1）∵用一块长为50cm、宽为30cm的长方形铁片制作一个无盖的盒子，在铁片的四个角截去四个相同的小正方形，
设小正方形的边长为xcm，
∴底面的长AB=（50-2x）cm，宽BC=（30-2x）cm，
故答案为：50-2x，30-2x；

（2）依题意，得：
（50-2x）（30-2x）=300
整理，得：x²-40x+300=0
解得：x₁=10，x₂=30（不符合题意，舍去）
当x₁=10时，盒子容积=（50-20）（30-20）×10=300（cm³）；

点评：此题主要考查了一元二次方程的应用，想象出立体图形的形状进而表示出侧面积是解题关键．