题目内容
18.一个圆锥的侧面展开图是半径为3,圆心角为120°的扇形,则这个圆锥的高为2$\sqrt{2}$.分析 易得扇形的弧长,除以2π即为圆锥的底面半径,根据母线长为3,利用勾股定理即可求得圆锥的高.
解答 解:圆锥的侧面展开图的弧长为:$\frac{120π×3}{180}$=2π,
∴圆锥的底面半径为2π÷2π=1,
∴该圆锥的高为:$\sqrt{{3}^{2}-{1}^{2}}$=2$\sqrt{2}$.
故答案为:2$\sqrt{2}$.
点评 此题考查了圆锥的计算,用到的知识点为:圆锥的侧面展开图的弧长等于圆锥的底面周长;圆锥的高,母线长,底面半径组成直角三角形.

练习册系列答案
 备战中考寒假系列答案
备战中考寒假系列答案
相关题目
9.使不等式x-1≥2与3x-7<8同时成立的x的整数值是( )
| A. | 3,4 | B. | 4,5 | C. | 3,4,5 | D. | 4 |
13.对于数据:6,3,4,7,6,0,9,下列判断中正确的是( )
| A. | 这组数据的平均数是6,中位数是6 | B. | 这组数据的平均数是5,中位数是6 | ||
| C. | 这组数据的平均数是6,中位数是7 | D. | 这组数据的平均数是5,中位数是7 |
10.下列运算正确的是( )
| A. | a2•a3=a6 | B. | (a3)2=a9 | C. | (-$\frac{1}{2}$)-2=4 | D. | (sin30°-π)0=0 |
8.下列各式正确的是( )
| A. | x2+x3=x5 | B. | x3•x2=2x5 | C. | x5÷x3=x2 | D. | (x5)2=x7 |
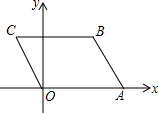 如图,已知A(4,0),B(3,3),以OA、AB为边作?OABC,则若一个反比例函数的图象经过C点,则这个反比例函数的表达式为y=-$\frac{3}{x}$.
如图,已知A(4,0),B(3,3),以OA、AB为边作?OABC,则若一个反比例函数的图象经过C点,则这个反比例函数的表达式为y=-$\frac{3}{x}$. 如图,⊙O是正方形ABCD的外接圆,点P在⊙O上,则∠APB=45°.
如图,⊙O是正方形ABCD的外接圆,点P在⊙O上,则∠APB=45°.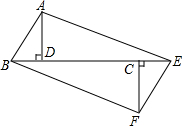 如图,已知△ABD和△CEF都是斜边为2cm的全等直角三角形,其中∠ABD=∠FEC=60°,且B、D、C、E都在同一直线上,DC=4.
如图,已知△ABD和△CEF都是斜边为2cm的全等直角三角形,其中∠ABD=∠FEC=60°,且B、D、C、E都在同一直线上,DC=4.