题目内容
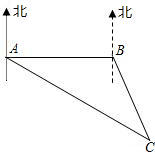台湾“华航”客机失事后，祖国大陆海上搜救中心立即通知位于A、B两处的上海救捞人局所属专业救助轮“华意”轮、“沪救12”轮前往出事地点协助搜索．接到通知后，“华意”轮测得出事地点C在A的南偏东60°，“沪救12”轮测得出事地点C在B的南偏东30度．已知B在A的正东方向，且相距100浬，分别求出两艘船到达出事地点C的距离．
分析：根据题意画出图形，将实际问题转化为解直角三角形的问题来解答，解答过程中要用到等腰三角形的性质．
解答：
解：如图：过C作CE⊥AE于E，过B作BF⊥CE于F．
则四边形AEFB是矩形
∵C在A的南偏东60°
∴∠2=60°，∠1=90°-∠2=90°-60°=30°
又因为点C在B的南偏东30°
所以∠3=30°
在Rt△ABG中，∠1=30°
则∠ABC=90°+30°=120°
于是∠BCG=180°-30°-120°=30°
根据等角对等边，BC=AB=100浬．
作BG⊥AC
则AG=AB•cos30°=50
浬
AC=50
×2=100
浬．
答：A到达出事地点C的距离100
浬，B到达出事地点C的距离100浬．
解：如图：过C作CE⊥AE于E，过B作BF⊥CE于F．则四边形AEFB是矩形
∵C在A的南偏东60°
∴∠2=60°，∠1=90°-∠2=90°-60°=30°
又因为点C在B的南偏东30°
所以∠3=30°
在Rt△ABG中，∠1=30°
则∠ABC=90°+30°=120°
于是∠BCG=180°-30°-120°=30°
根据等角对等边，BC=AB=100浬．
作BG⊥AC
则AG=AB•cos30°=50
| 3 |
AC=50
| 3 |
| 3 |
答：A到达出事地点C的距离100
| 3 |
点评：本题是一道实际问题，要利用解直角三角形的相关知识解答，通过此题可以使同学们体会到学好数学是多么重要．
练习册系列答案
智能训练练测考系列答案
相关题目
台湾“华航”客机失事后，祖国大陆海上搜救中心立即通知位于A、B两处的上海救捞人局所属专业救助轮“华意”轮、“沪救12”轮前往出事地点协助搜索．接到通知后，“华意”轮测得出事地点C在A的南偏东60°、“沪救12”轮测得出事地点C在B的南偏东30°．已知B在A的正东方向，且相距50海里，分别求出两艘船到达出事地点C的距离．
