题目内容
已知a为有理数，那么代数式|a-1|+|a-2|的取值有没有最小值？如果有，试求出这个最小值；如果没有，请说明理由．
考点：绝对值
专题：分类讨论
分析：根据绝对值的几何意义解答即可．
解答：解：有最小值．
理由：由绝对值的几何意义可知，就是要在数轴上求一点a，使它到1、2这2个点的距离和最小，
所以当1≤a≤2时，此式有最小值，最小值是1．
理由：由绝对值的几何意义可知，就是要在数轴上求一点a，使它到1、2这2个点的距离和最小，
所以当1≤a≤2时，此式有最小值，最小值是1．
点评：此题主要考查了绝对值，利用点与数轴的关系得出是解题关键．
练习册系列答案
习题精选系列答案
相关题目
如图，△ABC的面积是下列各组中的两个单项式不是同类项的是（ ）
| A、2a3b与-ba3 | ||||
| B、-3与0 | ||||
C、
| ||||
| D、6a2m与-9a2m |
下列分解因式正确的是（ ）
| A、a2+6a+5=a（a+6）+5 |
| B、（a-b）2+4ab=（a+b）2 |
| C、（a+1）（a+2）=a2+3a+2 |
| D、a3b-ab=ab（a2-1） |
下列运算正确的是（ ）
| A、6x3-5x2=x |
| B、（-2a）2=-2a2 |
| C、（a-b）2=a2-b2 |
| D、-2（a-1）=-2a+2 |
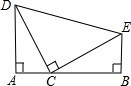已知：如图，在△CDE中，∠DCE=90°，CD=CE，直线AB经过点C，且点D、E在直线AB的同侧，在直线AB上点C的左、右两侧分别取点A、B，使得∠DAC=∠EBC=∠DCE．