题目内容
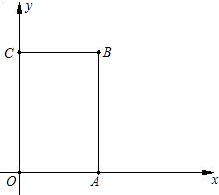
 如图,长方形OABC在直角坐标系中,A、C两点分别在第三象限和第一象限,点B在y轴的正半轴,OB=8,∠COx=60°,求A、B、C的坐标.
如图,长方形OABC在直角坐标系中,A、C两点分别在第三象限和第一象限,点B在y轴的正半轴,OB=8,∠COx=60°,求A、B、C的坐标.
 解:∵∠COx=60°,
解:∵∠COx=60°,∴∠BOC=90°-60°=30°,
∵OB=8,
∴OC=OB•cos30°=8×
 =4
=4 ,
,BC=
 OB=
OB= ×8=4,
×8=4,过点A作AD⊥x轴于D,过点C作CE⊥⊥x轴于E,
则∠AOD=90°-∠COx=90°-60°=30°,
OA=BC=4,
在Rt△AOD中,OD=OA•cos30°=4×
 =2
=2 ,
,AD=
 OA=
OA= ×4=2,
×4=2,在Rt△COE中,OE=
 OC=
OC= ×4
×4 =2
=2 ,
,CE=OC•sin60°=4
 ×
× =6,
=6,∴点A(-2
 ,2),B(0,8),C(2
,2),B(0,8),C(2 ,6).
,6).分析:先求出∠BOC=30°,解直角三角形求出OC,BC,过点A作AD⊥x轴于D,过点C作CE⊥⊥x轴于E,然后求出OD、AD,OE、CE的长度,再写出各点的坐标即可.
点评:本题考查了坐标与图形性质,矩形的性质,主要利用了解直角三角形,作辅助线构造出直角三角形是解题的关键.

练习册系列答案
 红果子三级测试卷系列答案
红果子三级测试卷系列答案 课堂练加测系列答案
课堂练加测系列答案 轻松课堂单元测试AB卷系列答案
轻松课堂单元测试AB卷系列答案
相关题目
 3,0),(0,5),点B在第一象限内.
3,0),(0,5),点B在第一象限内.
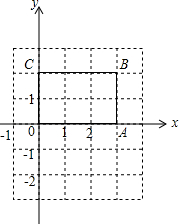 如图,长方形OABC中,O为平面直角坐标系的原点,点A、C的坐标分别为A(3,0),C(0,2),点B在第一象限.
如图,长方形OABC中,O为平面直角坐标系的原点,点A、C的坐标分别为A(3,0),C(0,2),点B在第一象限.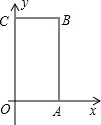 如图,长方形OABC中,O为平面直角坐标系的原点,A,C两点的坐标分别为(3,0),(0,5),点B在第一象限内.
如图,长方形OABC中,O为平面直角坐标系的原点,A,C两点的坐标分别为(3,0),(0,5),点B在第一象限内.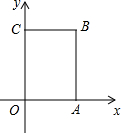 如图,长方形OABC中,O为平面直角坐标系的原点,A,C两点的坐标分别为(3,0),(0,5),点B在第一象限内.
如图,长方形OABC中,O为平面直角坐标系的原点,A,C两点的坐标分别为(3,0),(0,5),点B在第一象限内.