题目内容
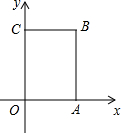 如图,长方形OABC中,O为平面直角坐标系的原点,A,C两点的坐标分别为(3,0),(0,5),点B在第一象限内.
如图,长方形OABC中,O为平面直角坐标系的原点,A,C两点的坐标分别为(3,0),(0,5),点B在第一象限内.(1)写出点B的坐标;
(2)若过点C的直线CD交AB于点D,且把AB分为4:1两部分,写出点D的坐标;
(3)在(2)中,计算四边形OADC的面积.
分析:(1)根据矩形的性质求出点B的横坐标与纵坐标即可得解;
(2)分AD是4份和1份两种情况讨论求出AD的长,从而得到点D的坐标;
(3)根据梯形的面积公式列式计算即可得解.
(2)分AD是4份和1份两种情况讨论求出AD的长,从而得到点D的坐标;
(3)根据梯形的面积公式列式计算即可得解.
解答:解:(1)∵A,C两点的坐标分别为(3,0),(0,5),
∴点B的横坐标为3,纵坐标为5,
∴点B的坐标为(3,5);
(2)若AD为4份,则AD=5×
=4,
此时点D的坐标为(3,4),
若AD为1份,则AD=5×
=1,
此时点D的坐标为(3,1),
综上所述,点D的坐标为(3,4)或(3,1);
(3)AD=4时,四边形OADC的面积=
(4+5)×3=
,
AD=1时,四边形OADC的面积=
(1+5)×3=9,
综上所述,四边形OADC的面积为
或9.
∴点B的横坐标为3,纵坐标为5,
∴点B的坐标为(3,5);
(2)若AD为4份,则AD=5×
| 4 |
| 1+4 |
此时点D的坐标为(3,4),
若AD为1份,则AD=5×
| 1 |
| 1+4 |
此时点D的坐标为(3,1),
综上所述,点D的坐标为(3,4)或(3,1);
(3)AD=4时,四边形OADC的面积=
| 1 |
| 2 |
| 27 |
| 2 |
AD=1时,四边形OADC的面积=
| 1 |
| 2 |
综上所述,四边形OADC的面积为
| 27 |
| 2 |
点评:本题考查了坐标与图形性质,主要利用了矩形的性质,平面直角坐标系,注意要分情况讨论.

练习册系列答案
 新题型全程检测期末冲刺100分系列答案
新题型全程检测期末冲刺100分系列答案
相关题目
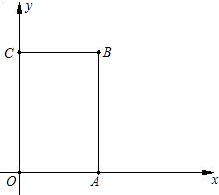 3,0),(0,5),点B在第一象限内.
3,0),(0,5),点B在第一象限内.
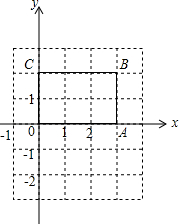 如图,长方形OABC中,O为平面直角坐标系的原点,点A、C的坐标分别为A(3,0),C(0,2),点B在第一象限.
如图,长方形OABC中,O为平面直角坐标系的原点,点A、C的坐标分别为A(3,0),C(0,2),点B在第一象限.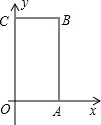 如图,长方形OABC中,O为平面直角坐标系的原点,A,C两点的坐标分别为(3,0),(0,5),点B在第一象限内.
如图,长方形OABC中,O为平面直角坐标系的原点,A,C两点的坐标分别为(3,0),(0,5),点B在第一象限内.