题目内容
 如图,CD是经过∠BCA顶点C的一条直线,CA=CB.E、F分别是直线CD上两点,且∠BEC=∠CFA=∠α.直线CD经过∠BCA的内部,且E、F在射线CD上,∠BCA+∠α=180°.请你说明:
如图,CD是经过∠BCA顶点C的一条直线,CA=CB.E、F分别是直线CD上两点,且∠BEC=∠CFA=∠α.直线CD经过∠BCA的内部,且E、F在射线CD上,∠BCA+∠α=180°.请你说明:(1)BE=CF;
(2)EF=|BE-AF|.
考点:全等三角形的判定与性质
专题:证明题
分析:根据三角形的内角和定理可得∠BCE+∠α+∠CBE=180°,从而得到∠CBE=∠ACF,再利用“角角边”证明△BCE和△CAF全等,根据全等三角形对应边相等可得BE=CF,AF=CE,从而得证.
解答:证明:在△BCE中,∠BCE+∠α+∠CBE=180°,
∵BCA+∠α=180°,
∴∠CBE=∠ACF,
在△BCE和△CAF中,
,
∴△BCE≌△CAF(AAS),
∴(1)BE=CF,
(2)AF=CE,
∴EF=|CF-CE|=|BE-AF|.
∵BCA+∠α=180°,
∴∠CBE=∠ACF,
在△BCE和△CAF中,
|
∴△BCE≌△CAF(AAS),
∴(1)BE=CF,
(2)AF=CE,
∴EF=|CF-CE|=|BE-AF|.
点评:本题考查了全等三角形的判定与性质,三角形的内角和定理,熟练掌握三角形全等的判断方法并求出∠CBE=∠ACF是解题的关键.

练习册系列答案
 金钥匙试卷系列答案
金钥匙试卷系列答案
相关题目
|-32|的相反数是( )
| A、-3 | B、3 | C、-9 | D、9 |
不等式组
的解集是x>3,则n的取值范围是( )
|
| A、n>3 | B、n≥3 |
| C、n=3 | D、n≤3 |
若规定一种特殊运算※为:a※b=ab-
,则(-1)※(-2)=( )
| a |
| b |
A、
| ||
B、-
| ||
C、
| ||
D、-
|
实验中学2009年中考上线451人,近三年中考上线共1567人,问:2010年、2011年中考上线平均每年增长率是多少?设平均增长率为x,则列出下列方程正确的是( )
| A、451(1+2x)=1567 |
| B、451+451(1+2x)=1567 |
| C、451(1+x)2=1567 |
| D、451+451(1+x)+451(1+x)2=1567 |
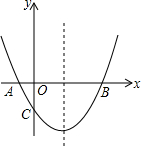 如图,抛物线经过A(-1,0),B(5,0),C(0,-
如图,抛物线经过A(-1,0),B(5,0),C(0,-